kjslajslaj asjlaksj jlasjlakjslj kjslajslaj asjlaksj jlasjlakjslj kjslajslaj asjlaksj jlasjlakjslj kjslajslaj asjlaksj jlasjla

Ein beliebtes Kartenspiel in der Schweiz ist der Jass. Es wird mit 36 Karten gespielt, bei denen also die Zweier, Dreier, Vierer und Fünfer fehlen (Bridge hat 52 Karten). Bei einigen dieser Spiele wie Schieber und Bieter spielt die Möglichkeit, weisen zu dürfen, eine Rolle.

Weismöglichkeiten sind

o Dreiblatt (3-er Sequenz)

o Fünfzig (4-er Sequenz)

o Hundert in 4 Blatt (4 Damen z.B.)

o Hundert sonst (5-er, 6-er oder 7-er Sequenz)

o Hunderfünfzig (4 Nel)

o Zweihundert (4 Bauern)

Unter Sequenz versteht man eine ununterbrochene Kartenreihe in der Ordnung As, König, Dame, Bauer, Zehn, Neun, Acht, Sieben und Sechs.

Beim Schieber erhält jeder Spieler 9 Karten.

In diesen Weisregeln gibt es ein paar auffallende Ungereimtheiten

o Die 4 Bauern, für die man 200 Punkte bekommt, sind mehr als 3 mal häufiger als der 6-blätterige Hunderter!

o Die 4 Nel geben nur 150 Punkte, obwohl sie nicht häufiger sind als die 4 Bauern.

o Ein 4-blätteriger Hunderter ist 1.55 mal häufiger als der 5-blätterige und gibt trotzdem gleichviel Punkte.

Dafür und für

o In 73.6% der Fälle kann man nichts weisen

o In 22.5% der Fälle hat man ein Dreiblatt

wollen wir hier die Begründung liefern.

Wir beginnen mit dem einfacheren Berechnen der Wahrscheinlichkeit für vier gleich hohe Karten.

Vier Bauern

Nehmen wir zunächst die 4 Bauern. Dass ich sie gerade in den ersten 4 Karten erhalte, hat die Wahrscheinlichkeit

Ich kann sie aber z.B. auch in der der 2., 4., 6. und 9. Karte erhalten. Dafür beträgt die Wahrscheinlichkeit

d.h. NICHT in der ersten, in der zweiten, NICHT in der dritten u.s.w.

Es stellt sich heraus, dass die Wahrscheinlichkeit immer die gleiche ist, unabhängig von der Reihenfolge des Eintreffens. Solche verschiedene Reihenfolgen gibt es genau

Irgendeine dieser Reihenfolgen muss eintreffen, sodass wir die Wahrscheinlichkeiten alle zusammenzählen dürfen

Dies ist die Wahrscheinlichkeit in 9 Karten 4 Bauern zu haben.

Der Fall ist aequivalent zu einer Urne mit s=4 schwarzen und w=32 weissen Kugeln, aus der man ohne Zurücklegen n=9 mal zieht. Die Formel für die Wahrscheinlichkeit, k=4 schwarze Kugeln zu erwischen, lautet dann

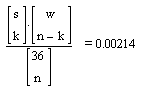
Für vier Nelle (9-er) ist die Wahrscheinlichkeit natürlich gleich gross.

Dagegen ist die Wahrscheinlichkeit einen vierblätterigen Hunderter zu bekommen viermal grösser, weil dazu vier Varianten vorhanden sind, nämlich Asse, Könige, Damen oder Zehner

Wahrscheinlichkeit für die Stöcke

Der Fall ist aequivalent zu einer Urne mit s=2 schwarzen und w=34 weissen Kugeln, aus der man ohne Zurücklegen n=9 mal zieht. Die Formel für die Wahrscheinlichkeit, k=2 schwarze Kugeln zu erwischen, lautet dann

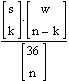= 5.71 %

Dreiblatt

Es gibt fast 100 Millionen verschiedene Arten 9 Karten aus 36 zugeteilt zu bekommen

Diese alle aufzulisten und zu Bestimmung von Waahrscheinlichkeiten die günstigen Fälle zu zählen wäre sehr mühsam.

Glücklicherweise lässt sich eine Aufspaltung der Aufgabenstellung vornehmen.

Man zunächst nach den Wahrscheinlichkeiten für verschiedenen Farbverteilungen (type de main) fragen.

Anschliessend brauchen die günstigen Fälle nur noch in Mengen von maximal

Elementen gezählt zu werden, weil, wenn für eine bestimmte Farbe (§ ¨ © ª) n ≤ 9 Karten aus den 9 Karten As, König, .. Sieben und Sechs gezogen werden, dies auf

Arten geschehen kann und

am grössten sind .

Farbverteilungen

Die Farbverteilung sei mit abcd bezeichnet, wobei a z.B. die Anzahl Pik, b die Anzahl Kreuz, c die Anzahl Herz und d die Anzahl Karo bedeuten soll.

Die a Piks kann ich auf

Arten bekommen. Dasselbe gilt für die drei anderen Farben, sodass die Farbverteilung auf

Arten realisiert werden kann.

Jetzt ist aber zusätzlich darauf zu achten, dass die Zuordnung a = Pik, b=Kreuz, u.s.w. willkürlich war. Jede Farbverteilung ist 4! = 24 mal häufiger. Dies gilt nicht ganz, weil bei gleichhäufigen Farben eine Permutaion in diesen Farben nichts ausmacht. Deshalb muss man korrigierend dividieren.

Wenn zwei Farben gleichhäufig sind, muss durch 2 geteilt werden, wenn drei Farben gleichhäufig sind, muss durch 3! = 6 geteilt werden und wenn vier Farben gleichhäufig sind, muss durch 4! = 24 geteilt werden (a, b, g).

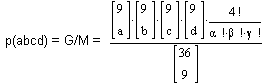
Es gibt nur 18 verschiedene Farbverteilungen. Wir haben sie hier nach ihrer Häufigkeit p geordnet. Demnach ist zweimal eine Farbe à 3 Karten, dann eine Farbe à 2 Karten sowie eine Farbe mit einer einzigen Karte die häufigste Farbverteilung.

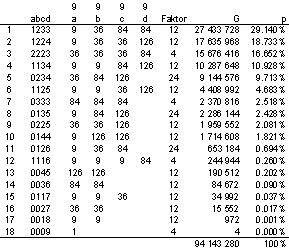
Figure 1 Farbverteilungen

Diese Tabelle kann man einfacher mit folgender Ueberlegung erzeugen.

Il suffit de décomposer l'urne (le jeu de 36 cartes) en 4 catégories : § ¨ © ª de chacune 9 cartes et l'on obtient par la formule polyhypergéométrique les résultats.

Häufigkeit von Sequenzen in maximal 9 gleichfarbigen Karten

Wir zählen nun in den maximal 126 langen Listen der Kombinationen genau ab, wie oft die einzelnen Sequenzen auftreten.

Das Resultat ist das folgende.

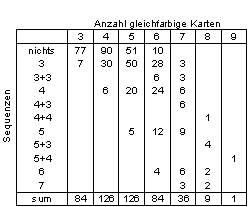
Figure 2 Die explizit abgezählten Häufigkeiten von Sequenzen für gegebene Anzahl Karten

Die Details für diese Tafel sehen wie folgt aus.

(A) Für acht gleiche Farben

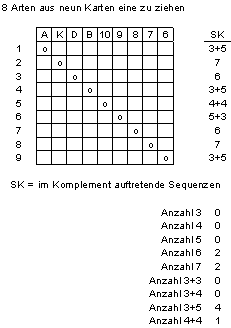
Figure 3 Sequenzen in Achtfärber

(B) Für sieben gleiche Farben

Figure 4 Sequenzen in Siebenfärber (Teil a)

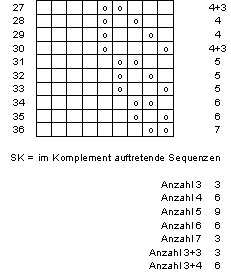
Figure 5 Sequenzen in Siebenfärber (Teil b)

Figure 6 Sequenzen in 6- oder 3-Färber (Teil a)

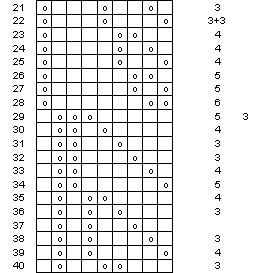
Figure 7 Sequenzen in 6- oder 3-Färber (Teil b)

Figure 8 Sequenzen in 6- oder 3-Färber (Teil c)

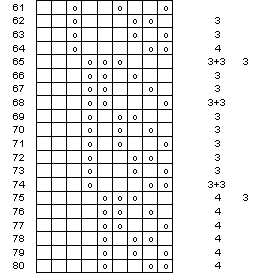
Figure 9 Sequenzen in 6- oder 3-Färber (Teil d)

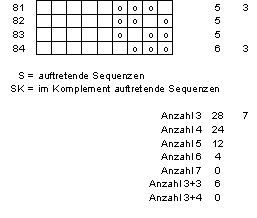
Figure 10 Sequenzen in 6- oder 3-Färber (Teil e)

(D) Für fünf oder vier gleiche Farben

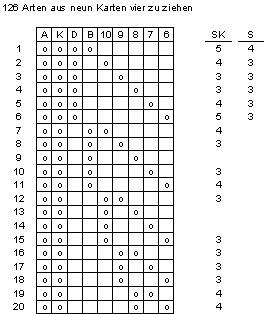
Figure 11 Sequenzen in 5- oder 4-Färber (Teil a)

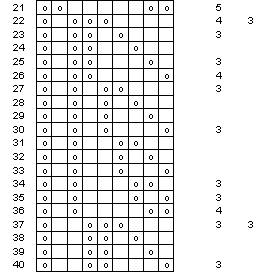
Figure 12 Sequenzen in 5- oder 4-Färber (Teil b)

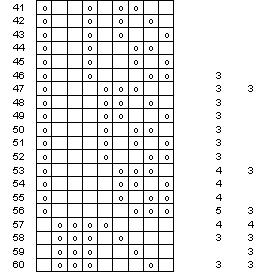
Figure 13 Sequenzen in 5- oder 4-Färber (Teil c)

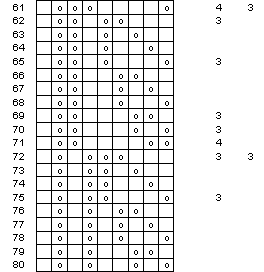
Figure 14 Sequenzen in 5- oder 4-Färber (Teil d)

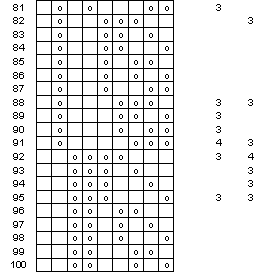
Figure 15 Sequenzen in 5- oder 4-Färber (Teil e)

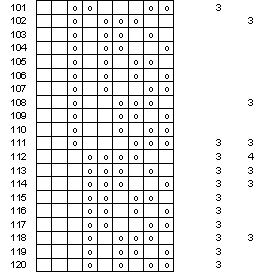
Figure 16 Sequenzen in 5- oder 4-Färber (Teil f)

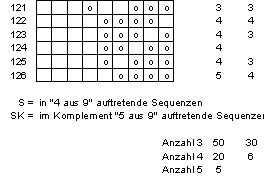
Figure 17 Sequenzen in 5- oder 4-Färber (Teil g)

Verbinden zur Gesamtwahrscheinlichkeit

Wahrscheinlichkeit für genau 1 mal Dreiblatt

▬ in der Farbverteilung 1233 (mit der Wahrscheinlichkeit 0.2914 aus Figur 1) muss das Dreiblatt im ersten Dreifärber (7 mal in 84 Fällen siehe Figur 2) und nicht im Zweiten oder nicht im ersten Dreifärber und im Zweiten auftreten

▬ in der Farbverteilung 1224:

nur im Vierfärber möglich

▬ in der Farbverteilung 2223:

nur im Dreifärber möglich

▬ in der Farbverteilung 1134:

▬ in der Farbverteilung 0234:

▬ in der Farbverteilung 1125:

▬ in der Farbverteilung 0333:

Das Dreiblatt muss im einen Dreifärber (von 3) und nicht in den zwei andern auftreten

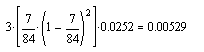
▬ in der Farbverteilung 0135:

▬ in der Farbverteilung 0225:

▬ in der Farbverteilung 0144:

▬ in der Farbverteilung 0126:

▬ in der Farbverteilung 1116:

▬ in der Farbverteilung 0045:

und ein paar vernachlässigbare Terme, was zusammen für die Wahrscheinlichkeit für genau 1 mal Dreiblatt

21.50 % ergibt.

Wahrscheinlichkeit für Fünfzig

▬ in den Farbverteilungen 1224, 1134 und 0234 kommt der 4-Färber je einmal vor und darin die 4er Sequenz 6 mal

▬ in den Farbverteilungen 1125, 0135 und 0225 kommt der 5-Färber je einmal vor vor und darin die 4er Sequenz 20 mal

▬ in der Farbverteilung 0144:

▬ in den Farbverteilungen 0126 und 1116 kommt der 6-Färber je einmal vor und darin die 4er Sequenz 24 mal

▬ in der Farbverteilung 0045:

und ein paar vernachlässigbare Terme, was zusammen für die Wahrscheinlichkeit für "Fünfzig"

3.80 % ergibt.

Wahrscheinlichkeit für genau 2 mal Dreiblatt

▬ in der Farbverteilung 1233 mit der Wahrscheinlichkeit 0.2914 (aus Figur 1) muss das Dreiblatt im ersten und zweiten Dreifärber auftreten

▬ in der Farbverteilung 1134 ähnlich:

▬ in der Farbverteilung 0234 ähnlich:

▬ in der Farbverteilung 0333 muss das Dreiblatt in zwei von drei Dreifärbern auftreten und nicht im dritten

▬ in der Farbverteilung 0135:

▬ in der Farbverteilung 0144:

▬ in der Farbverteilung 0126 und 1116 kommt der 6-Färber je einmal vor und darin die 2 mal Dreiblatt 6 mal

▬ in der Farbverteilung 0045:

▬ in der Farbverteilung 0036 muss ein Dreiblatt im 3-Färber und eines im 6-Färber liegen oder beide im 6-Färber und keines im 3-Färber

▬ in der Farbverteilung 0117 und 0027 kommt der 7-Färber je einmal vor und darin die 2 mal Dreiblatt 3 mal

und ein paar vernachlässigbare Terme, was zusammen für die Wahrscheinlichkeit für genau zweimal Dreiblatt

0.94 % ergibt.

Wahrscheinlichkeit für 5-blätterigen Hunderter

▬ in den Farbverteilungen 1125, 0225, 0135 und 0045 kommt der 5-Färber je einmal vor und darin die 5er Sequenz 5 mal

▬ in den Farbverteilungen 1116, 0126 und 0036 kommt der 6-Färber je einmal vor und darin die 5er Sequenz 12 mal

▬ in der Farbverteilung 0117 und 0027

und ein paar vernachlässigbare Terme, was zusammen für die Wahrscheinlichkeit für den 5-blätterigen Hunderter

0.536 % ergibt.

Wahrscheinlichkeit für 6-blätterigen Hunderter

▬ in den Farbverteilungen 1116, 0126 und 0036 kommt der 6-Färber je einmal vor und darin die 6er Sequenz 4 mal

▬ in den Farbverteilungen 0117 und 0027 kommt der 7-Färber je einmal vor und darin die 6er Sequenz 6 mal

▬ in der Farbverteilung 0018 und 0009 sehr kleine Werte:

und kleiner

was zusammen für die Wahrscheinlichkeit für den 6-blätterigen Hunderter

0.06 % ergibt.

Wahrscheinlichkeit für Fünfzig und Dreiblatt

▬ in der Farbverteilung 1134

▬ in der Farbverteilung 0234

▬ in der Farbverteilung 0144

▬ in der Farbverteilung 0135

▬ in der Farbverteilung 0045

▬ in der Farbverteilung 0036

was zusammen für die Wahrscheinlichkeit für Fünfzig und Dreiblatt

0.146 % ergibt.

Wahrscheinlichkeit für 2 mal Fünfzig

▬ in der Farbverteilung 0144

▬ in der Farbverteilung 0045

▬ in der Farbverteilung 0018

was zusammen für die Wahrscheinlichkeit für 2 mal Fünfzig

0.0046 % ergibt.

Wahrscheinlichkeit für Hundert und Dreiblatt

▬ in der Farbverteilung 0045

▬ in der Farbverteilung 0018

was zusammen für die Wahrscheinlichkeit für Hundert und Dreiblatt

0.0024 % ergibt.

Wahrscheinlichkeit für Hundert und Fünfzig

Wahrscheinlichkeit für 7-blätterigen Hunderter

▬ in der Farbverteilung 0027 und 0117

▬ in der Farbverteilung 0018

was zusammen für die Wahrscheinlichkeit für den 7-blätterigen Hunderter

0.0052 % ergibt.

home