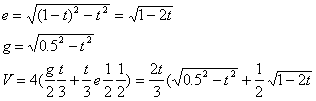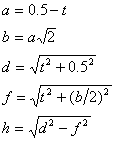Es ist bemerkenswert, dass aus zwei quadratischen Papieren stückweise flache Kissen (Polyeder) gefaltet werden können. Im allgemeinen sind die Abwicklungen von Polyedern keineswegs einfache Quadrate.

Ich habe sechs Arten von Polyederkissen untersucht. Ausgehend von diesen Arten kann man sehr viele andere Polyederkissen bauen, weil jede konvexe Spitze abgeschnitten und nach innen gespiegelt werden kann. Solche Variationen sind aber bezüglich Volumen immer unterlegen.

Kissen vom Typ I

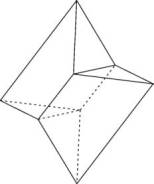
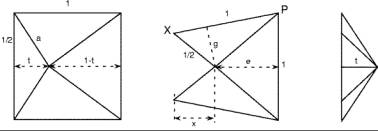
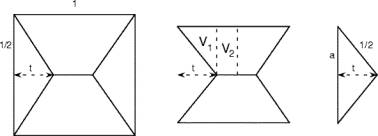
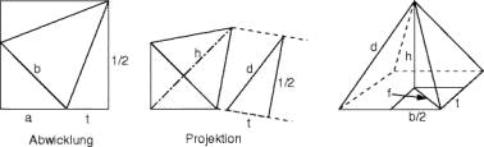
Die einzelnen Kissen dieser Familie können mit dem Parameter t charakterisiert werden, der den Abstand des vierkantigen Knickpunktes vom Rand des Ausgangsquadrates (mit Seitenlänge 1) misst.

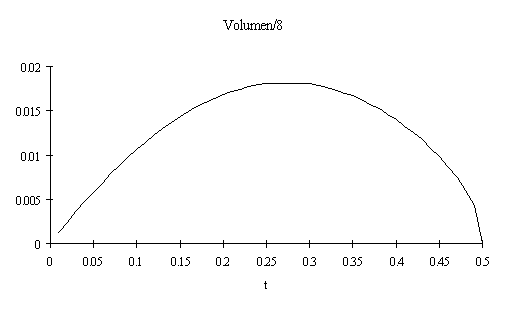
t kann zwischen 0 und 0.5 varieren. Nicht ganz in der Mitte, bei 0.273, wird das Volumen maximal. Es beträgt 0.1454. Das gezeigte Kissen ist dieses volumenoptimale.

Das Volumens hängt wie folgt vom Parameter t ab (siehe Anhang)

Hier die dazugehörige Kurve

Die oberflächengleiche Kugel hat das Volumen 0.266 und der oberflächengleiche Würfel das Volumen 0.192.

Wenn man diese Kissen zu Röhren mit rautenförmigem Querschnitt zusammenlegt und dann mit den Röhren den Raum füllt, ergibt sich ein Füllgrad von rund 63.6%.

Die Rautenwinkel betragen spitz=66.2°, stumpf=113.8°. Der "Kehlwinkel" ist gleich gross wie der stumpfe Rautenwinkel!

Wir zeigen aus der gleichen Kissenfamilie zwei nicht optimale Kissen, die zu den t-Werten 0.136 und 0.410 gehören und ein kleineres Volumen von 0.1071 bzw. 0.1063 haben

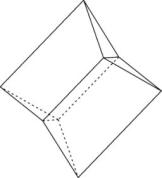
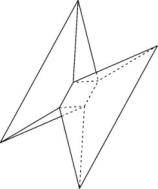
Variante zum Kissen vom Typ I

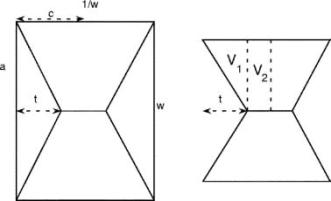
Wenn von einem Rechteck mit der Fläche 1 und dem Formparameter w ausgegangen wird (Seitenverhältnis 1/w : w), ergibt sich folgende Formel für das Volumen (siehe Anhang)

Hier die dazugehörige Kurve

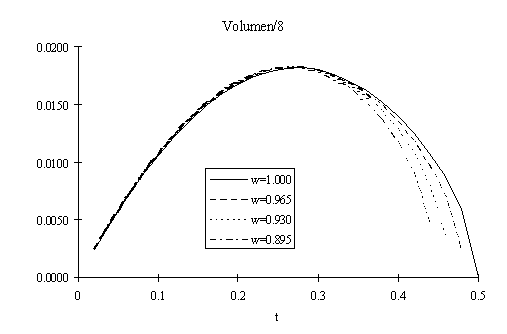
Das optimale Volumen wird hier bei w=0.9306 und t=0.269 erreicht und ist nur unwesentlich grösser als beim Quadrat: 0.1462 statt 0.1454.

Die Seite muss parallel zum Rist länger sein (107.5%).

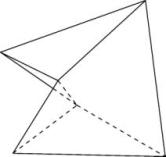
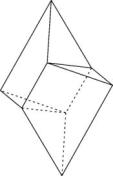
Es gibt eine interessante Verbindung zum Tetraeder.

Wenn man von der Variante des Kissens vom Typ I ausgeht, die ein optimales Doppelrechteck (und nicht Doppelquadrat) mit Fläche 2 als Abwicklung hat, und das Kissen in der quadratischen Taille um 90° verdreht, erhält man ein reguläres Tetraeder! Es hat deshalb auch genau des Volumen des oberflächengleichen Tetraeders 0.1462. (Hinweis von W.Bürger, Karlsruhe)

Hier die Illustration dazu.

Kissen vom Typ II

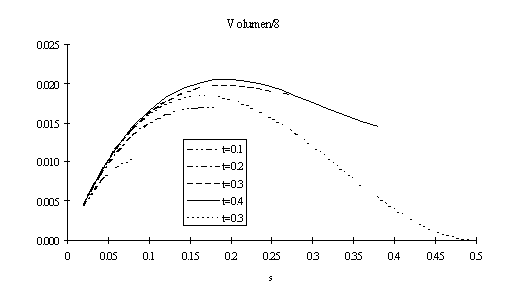
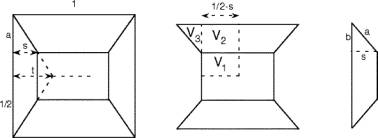
Die einzelnen Kissen dieser Familie können mit zwei Parametern t und s charakterisiert werden, von denen s den Abstand des vierkantigen Knickpunktes vom Rand des Ausgangsquadrates (mit Seitenlänge 1) misst und t den Abstand des Schnittpunktes des Eckfalzes mit der Mittenlinie des Quadrates vom Rand des Ausgangsquadrates.

t kann wieder zwischen 0 und 0.5 varieren und s dann jeweils zwischen 0 und t.

Das Volumens hängt wie folgt von den beiden Parametern ab (siehe Anhang)

und wird für t=0.3982 und s=0.1930 maximal, nämlich 0.1641. Es ist grösser als das Volumen von Kissen Typ I (0.1454), aber kleiner als das des oberflächengleichen Würfels (0.192).

Das gezeigte Kissen ist das volumenoptimierte.

Wenn man diese Kissen zu Röhren mit sechseckigem Querschnitt zusammenlegt und dann mit den Röhren den Raum füllt, ergeben sich zwei Füllgrade.

Art links:

Art rechts:

Also wenig mehr als bei Typ I (63.6%).

Bei t=0.5 wird auch die bisher nicht senkrechte Seite senkrecht und die Eckentetraeder verlieren jegliches Volumen. Sie können an das übrige Volumen angeschmiegt werden und wir haben das vertraute Bild des mit Packpapier eingehüllten Quaders. Weil das Kissen vom Typ II mit t=0.5 ein Quader ist, wird sein Füllgrad 100%.

Mit den Parametern t=0.5 und s=0.25 erhalten wir ein Kissen mit genau quadratischem Querschnitt (Projektion). Es hat das Volumen 0.1250.

Kissen vom Typ III

Die einzelnen Kissen dieser Familie können mit dem Parameter t charakterisiert werden, der den Abstand des vierkantigen Knickpunktes vom Rand des Ausgangsquadrates (mit Seitenlänge 1) misst.

t kann nur zwischen 0 und 0.433 varieren. Bei diesem Grenzwert schliesst sich die einspringende Konkavität (der nach innen ragende Falz hat kein Volumen mehr). Der Grenzwert berechnet sich aus der Gleichung (siehe Anhang)

Bei t=0.345, wird das Volumen maximal. Es beträgt 0.1473. Also etwas mehr als beim Kissen vom Typ I. Das gezeigte Kissen ist dieses volumenoptimale.

Das Volumen hängt wie folgt vom Parameter t (0 < t < 0.433) ab (siehe Anhang)

Formel 1:

Insbesondere beträgt das Volumen beim Grenzwert t=0.433 genau 1/8.

Wenn t Werte annimmt zwischen 0.433 und 0.500, haben wir immer noch reelle Polyederkissen. Man kann diese Kissen auch noch zum Typ III zählen. Ab t > 0.433 steht der nach innen ragende, leere Falz nicht mehr senkrecht und schmiegt sich bei t = 0.500 an eine Seite der pyramidenförmigen Kissenhälfte an, die ab t=0.433 ein gleichseitiges Dreieck mit Seitenlänge 1 als Grundriss hat.

Das Volumen muss dann für t zwischen 0.433 und 0.500 anders berechnet werden (siehe Anhang)

Formel 2:

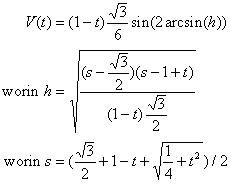
Insbesondere ist

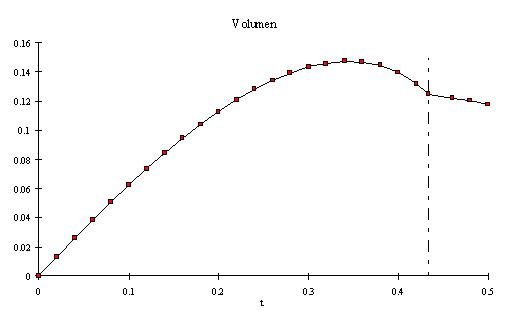
Formel 1 und 2 haben für t=0.433 den gleichen Wert, nämlich 1/8.

Die beiden Formeln für das Kissen vom Typ III ergeben folgende Kurve

Das Regelflächenkissen

Die Polyederkissen vom Typ I und II können als Spezialfälle eines allgemeineren Typs aufgefasst werden, bei dem 2n einspringende Knicks vorhanden sind. Typ I hat 2 und Typ II 4 solche Knicks.

Diese Polyederkissen mit 2 Symmetrien existieren alle. Die zusätzlichen Knicks können alle dazu verwendet werden das Volumen zu vergrössern.

Bei beliebig viele Knicks kommt man zum Regelflächenkissen. Es hat weiterhin definitionsgemäss ein Quadrat als Abwicklung. Das Kissen wird durch 3 Regelflächen begrenzt. Es ist längentreu kartografierbar.

Wenn man ein Quadrat mit seinen 2 Diagonalen vierteilt, so führen jene Kurven in einem solchen Viertel zu einem reellen Kissen, die in einer Ecke starten und in der andern enden und deren Richtung nie die Richtung der Diagonalen überschreiten.

Welches ist die Kurve, die zum grössten Volumen führt?

Die einfachste Kurve, die im genannten Viertel liegt und in den Ecken endet, ist der Kreisbogen, dessen Kreiszentrum in der Mitte eines Nachbarquadrates liegt.

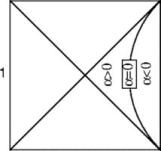
Die Kurve startet mit 45° in der Ecke des abgewickelten Quadrates, was zur Folge hat, dass die Tangente der entsprechenden Raumkurve an diesem Punkte senkrecht steht (bei waagrecht liegendem Kissen) und dass die Hauptregelfläche des Kissens nirgends eine Falte hat.

Das Volumen wird nicht mit einer geschlossenen Formel berechnet sondern numerisch angenähert (siehe Anhang).

Das Volumen des 'Kreiskissens' beträgt 0.1726. Es übertrifft erwartungsgemäss das optimale Volumen der Polyederkissen vom Typ II, das 0.164 beträgt.

Wir können das 'Kreiskissen' wie folgt verallgemeinern. Ausgehend vom Kreisbogen bilden wir gewichtete Mittel mit dem Rand des Quadratviertels

Für diese kontinuierliche Familie von Kurven in der Abwicklung ergibt sich ein Volumen, das für a=-1 und +1 verschwindet. Dazwischen wird das Volumen optimal bei a=0.056 und nicht bei a=0! Es beträgt dann 0.1730. Die folgende Kurve zeigt die Abhängigkeit des Volumens vom Parameter a.

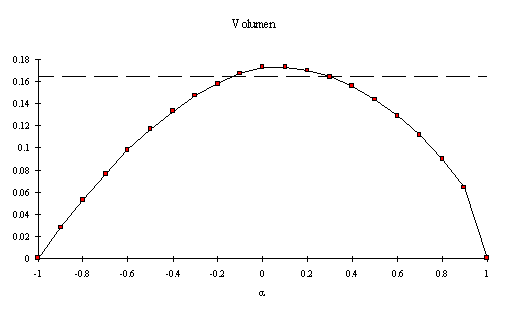
Das 'Kreiskissen' ist also nicht ganz optimal. Mit seinem Volumen von 0.1726 ist es dem optimalen Mittelkissen mit dem Volumen 0.1730, das in unserer Illustration gezeigt wird, nur unwesentlich unterlegen.

Mit einem kubischen Ansatz für die abgewickelte Knickkurve kann man das Volumen 0.1730 überbieten! Die anfängliche Steigung von 45° und eine Steigung null in der Mitte legen die kubische Kurve bis auf die Amplitude fest. Diese Amplitude habe ich so festgelegt, dass das Volumen des Kissens maximal ausfällt. Es erreicht 0.1741 und die entsprechende Amplitude ist 0.2218.

Ausgehend von Profilen, die Ellipsenform haben, konnte das Volumen noch einmal verbessert werden. Im Gegensatz zu den Kurven in der Abwicklung, muss die Profilkurve genau die Länge 2 haben. Dadurch kann die zweite Halbachse der Ellipse berechnet werden, wenn die erste frei gewählt wird. Ich habe die Potenzreihe bis zur 8. Potenz verwendet für die Ellipsenumfangformel. Die frei gewählte Halbachse habe ich in der Folge so festgelegt, dass das Kissenvolumen maximal wird. Es erreicht 0.1745 und die entsprechende Halbachse ist 0.2225.

Diesmal muss die Abwicklung y aus der Projektion Y berechnet werden:

Das Kissen mit Ellipsenprofil ist nicht ganz optimal für das Volumen! Wenn man alle 41 Punkte eines Polygons in der Abwicklung für das Volumen optimiert, kann man das Volumen etwas vergrössern. Die Optimierung ist recht heikel, weil der Radikand in der Gleichung für Y_i+1 leicht negativ werden kann. Dies geschieht genau dann, wenn die Kurve in der Abwicklung Orte mit einer Steigung grösser als eins hat. Der Excel-Solver geht mit Constraints nicht besonders geschickt um. Ich setzte deshalb den Arcustanges ein, um zu erzwingen. Jetzt konvergierte das Verfahren zuverlässig. In der Projektion (siehe Abbildung) ist die Kurve doch deutlich von der Ellipsenkurve unterscheidbar.

Weil die Kissen sehr spitz zulaufen, kommt es darauf an, wie die 41 Punkte verteilt sind. Beim Ellipsenkissen waren die Punkte gemäss Winkelparameter in der Projektion gleichmässig verteilt und nicht gemäss y_i in der Abwicklung. Durch Aenderung dieser Verteilung (mit einer Splineinterpolation) vergrössert sich das Ellipsenkissenvolumen von 0.1745 auf 0.1748.

Eine Optimierung eines Polygons mit 81 Punkten konvergierte auch und zeigt, dass man mit 41 Punkten die Volumen etwas überschätzt (um etwa 0.0001).

Wenn man mit den Kissen zunächst durch geeignetes Hintereinanderlegen Röhren mit hexagonalem Profil bildet und dann mit diesen Röhren den Raum füllt, erreicht man einen gewissen Füllgrad. Nur die zweite der folgenden Arten von Röhrenbildung bringt das hexagonale Profil:

Formel:

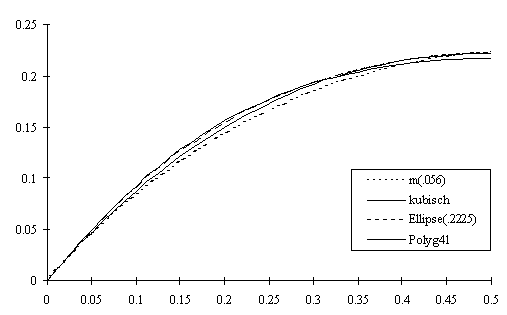
Eine Uebersicht über die bisher angetroffenen Regelflächenkissen sieht wie folgt aus. Die Kissen haben alle eine Breite von 1.

Höhe	Dicke	Volumen	Abwicklung	Projektion	Füllgrad
0.636	0.636	0.1471	-	Kreis	53.26%
0.848	0.414	0.1726	Kreis	-	62.01%
0.836	0.448	0.1730	Mittel	-	59.68%
0.822	0.444	0.1741	kubisch	-	61.34%
0.802	0.446	0.1748	-	Ellipse	66.20%
0.800	0.434	0.1749	Polygon	-	64.26%

Ich habe noch das Kissen mit kreisrundem Querschnitt dazugegeben. Es ist durchaus herstellbar, hat aber ein deutlich kleineres Volumen.

Hier die abgewickelten Kurven der diversen Regelflächenkissen

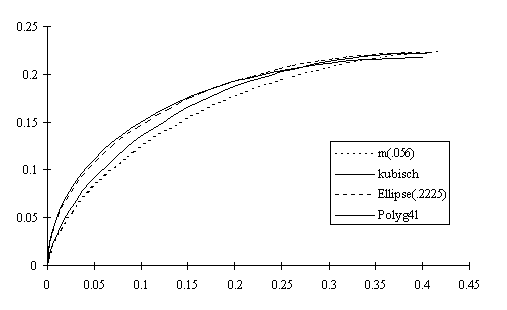
und die projizierten Kurven

Kissen und Gitter

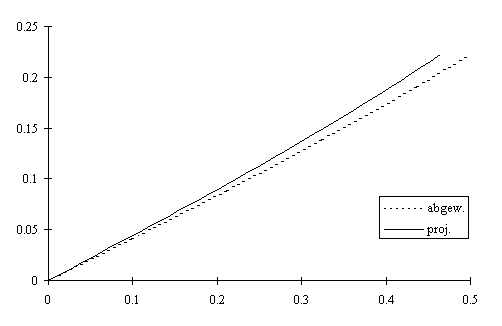
Für unsere Kissen gilt generell, dass die räumliche Knickkurve zwei gleiche Projektionen hat. Daraus ergibt sich, dass es eine dritte Projektion gibt, die hexagonal ausssieht und dass man mit den Kissen in der Ebene dieser hexagonalen Projektion ein Gitter aufbauen kann. Dies ist gleichbedeutend mit der Aussage, dass Zylinder mit dem nicht hexagonalen Profil des Kissens, die sich senkrecht durchdringen, bei Wegnahme des Durchdringungskörpers genau die Gestalt eines Kissens annehmen, dessen Abwicklung aus zwei Quadraten besteht.

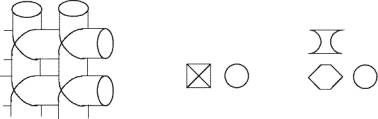
In der Mitte wird der Durchdringungskörper in Vorder-, Seiten- und Draufsicht gezeigt und rechts das Kissen.

Es lassen sich noch folgende Zusammenhänge zwischen den Volumen des Kissens KI, des Durchdringungskörpers DK, des Gitters GI und der Gittereinbettung GE angeben für das Ellipsenkissen (Breite b=1, Höhe h=0.802, Dicke d=0.446):

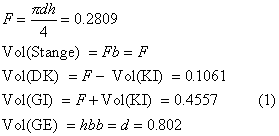
Anteil der Kissen am Gitter:

2*Vol(KI)/Vol(GI) = 76.7%

Anteil der Durchdringungskörper am Gitter:

Vol(DK)/Vol(GI) = 23.3%

Anteil des Gitter an der Gittereinbettung:

Vol(GI)/Vol(GE) = 56.8%

(1) entspricht der Tatsache, dass das Gitter dadurch aufgebaut werden kann, dass parallele Stangen mit Kissen verbunden werden.

Beim runden Kissen (Kreisquerschnitt) hat die Stange optimales Volumen, aber auch der DK ist gross. Mit zunehmender Exzentrizität werden beide kleiner. Vol(KI) = Vol(Stange)-Vol(DK) kann dabei ein Optimum durchlaufen.

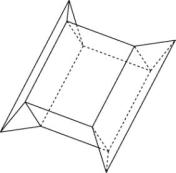
Kissen, die auf allen vier Seiten einspringen

Bisher wurden die Kissen höchstens an zwei gegenüberliegenden Seiten eingeknickt. Es stellt sich heraus, dass beim Typ I mit zusätzlichem Eindrücken der restlichen zwei Seiten etwas Volumen gewonnen werden kann!

Wenn wiederum das Ausmass des Eindrückens optimiert wird, erhalten wir folgendes Kissen

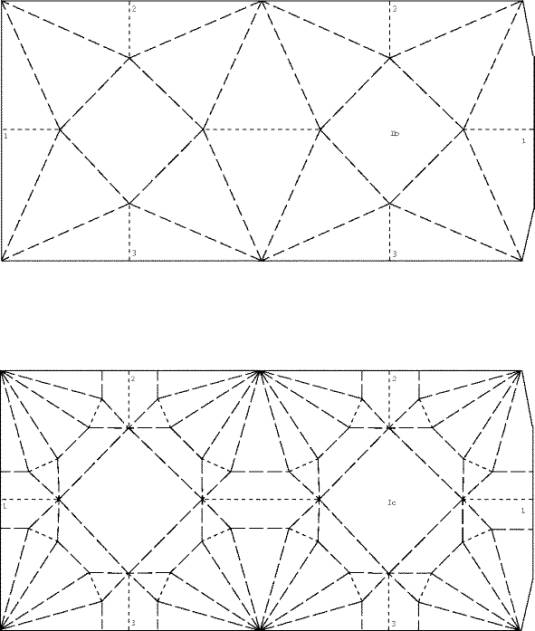
Kissen vom Typ Ib

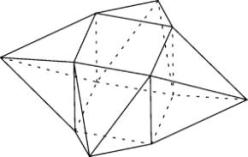
Es hat ein Volumen von 0.1756, also etwas mehr als die 0.1749 des besten bisherigen Regelflächenkissens.

Die einzelnen Kissen dieser Familie können mit dem Parameter t charakterisiert werden, der den Abstand des fünfkantigen Knickpunktes vom Rand des Ausgangsquadrates (mit Seitenlänge 1) misst.

t kann zwischen 0 und 0.5 varieren. Bei 0.219, wird das Volumen maximal. Die Formel für das Volumen lautet

Wie der Typ I zusammen mit Typ II zu einer Familie von Regelflächenkissen gezählt werden kann, in der ein Kissen mit dem Volumen 0.1749 auftrat, interessiert auch für den Typ Ib die entsprechende Verallgemeinerung.

Resultat:

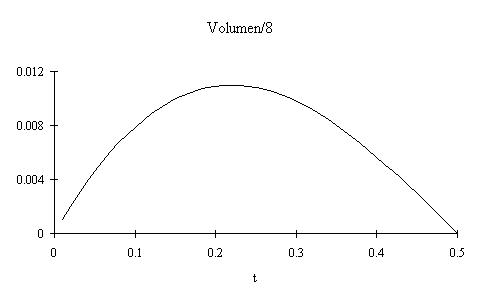
Das Volumen kann nur erstaunlich wenig von 0.17565 auf 0.17576 verbessert werden. Bei flachliegendem Kissen sind die Zipfel gegenüber dem Polyederkissen Ib vertikal leicht nach innen gewölbt und die Seitenwände der Zipfel leicht nach aussen. Die folgende Kurve zeigt das Ausmass dieser Wölbungen.

Kissen vom Typ Ic

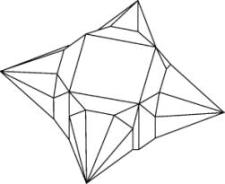
Indem beim Kissen Ib die Kanten der 4 Zipfel optimal eingedrückt werden und damit die Seiten der Zipfel nach aussen ausbauchen, kann man etwa 7.6% Volumen gewinnen!

Dies ist viel mehr als wir durch Umformung der Zipfelseiten zu Regelflächen gewinnen konnten.

Das ergibt ein neues Rekordkissen mit dem Volumen 0.1890, das zugleich eine gefällige Form hat.

Die Zipfel mit den eingedrückten Kanten sind der Kegelpyramide nachempfunden, die man gewinnt, wenn man ein halbes Oktogon zu einem Konus formt und seine 4 Seiten auf ein Quadrat am Boden klebt. Die Kegelpyramide hat eindeutig hypebolische und sphärische Flächenstücke und stresst das Papier (Dehnung), was an der Spannung des Papieres erkennbar ist. Diese Kegelpyramide ist damit nicht zu unserer Kissenkonkurrenz mit dehnungsfreiem Papier zugelassen.

Der Zipfel mit eingedrückten Kanten hingegen besteht stückweise aus lauter flachen (euklidischen) Facetten und ist damit dehnungsfrei.

Wir geben dem Zipfel mit eingedrückten Kanten nur zwei Parameter, die den Ort des Knickpunktes in der schmaleren Zipfelseite charakterisieren. Im Anhang lauten diese beiden Parameter t und s.

Ausgehend von diesem Punkt muss die konkave Faltung in der Abwicklung senkrecht zur Zipfelkante velaufen. Damit ergibt sich zwingend der Knickpunkt in der benachbarten, breiteren Zipfelseite, der gleich weit von der Kante liegt. Es ist bemerkenswert, dass die konkave Faltung im Raume nicht ganz parallel zum Zipfelboden verläuft im gegensatze zur konvexen Faltung auf der anderen Seite des Knickpunktes.

Im Anhang wird gezeigt, wie das Volumen abhängig von t und s berechnet werden kann und wie die Parameter optimiert werden können. Die optimalen Werte für das Rekordvolumen von 0.1890 sind cs=0.219, t=0.413 und s=0.0836.

Wir zeigen noch ein Kissen aus der Familie Typ 1c, das nicht optimal ist. Es hat ein Volumen von nur 0.1690 und die Parameter cs=0.30, t=0.312 und s=0.025.

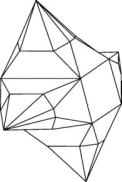
Netze zum Selberbauen der 6 Kissen

Kissen I und Kissen II.

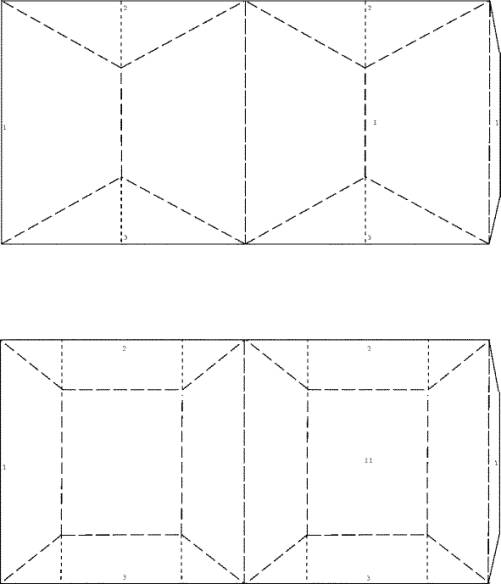
Kissen III und Kissen Regelflach.

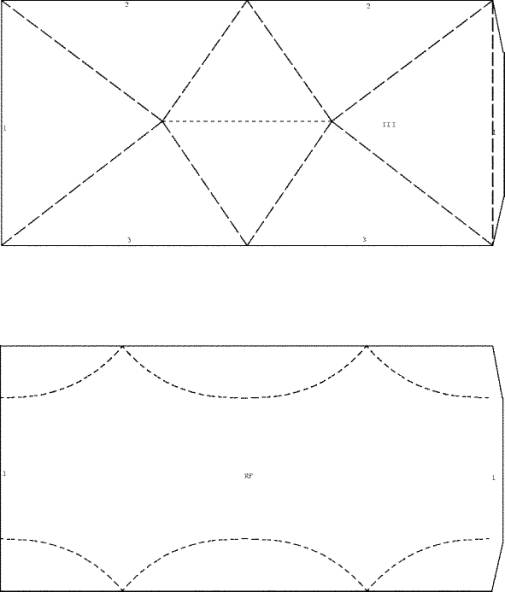
Kissen Ib und Kissen Ic.

Anhang zu den Kissen

Kissen vom Typ I

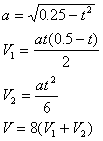
Kissen vom Typ Ivar

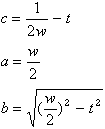
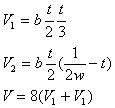
Kissen vom Typ II

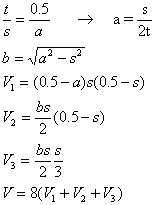
Kissen vom Typ III

Formel 1

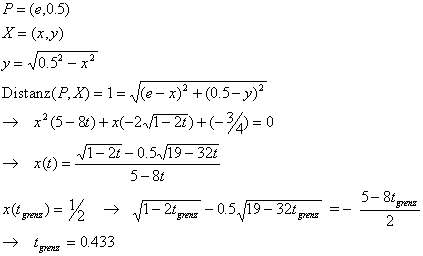
Für t>t_grenz

Formel 2

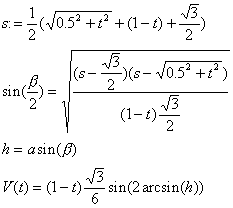
Kissen vom Typ Regelflach

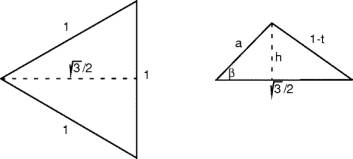
Bei der Berechnung des Volumens des Kissens sind folgende Formeln nützlich.

Es seien (x_i,y_i), i=1..n die n Punkte der Knickkurve in der Abwicklung,wobei der Koordinatenursprung in der Ecke des abgewickelten Quadrates liegen soll. Dann lauten die Koordinaten der räumlichen Kurve

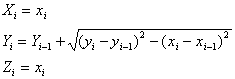
Das i-te Volumenelement ergibt sich wie folgt:

Für das Gesamtvolumen müssen die Volumenelemente für die Hälfte des Kreisboges aufsummiert und dann mit 8 multipliziert werden.

Kissen vom Typ Ib

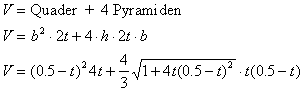
Dies ist gleichbedeutend mit

Kissen vom Typ Regelflach von Ib

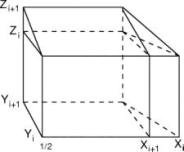
Der Uebergang von der abgewickelten Kurve (x,y) zur Raumkurve (X,Y,Z) ist komplizierter als im Falle des Regelflachs, wo die beiden einspringenden Seiten nicht benachbart waren.

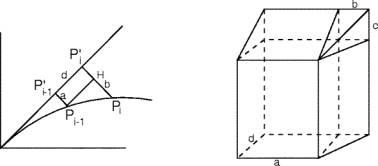
(x,y) seien wieder die Koordinaten in der Abwicklung und (X,Y,Z) die räumlichen Koordinaten der Knickkurve.

Das Kurvenstück (dx,dy) der Abwicklung muss soviel aus der Ebene Z=0 um die Achse senkrecht zu X=Y herausgedreht werden, dass dZ=dx wird. Dies erreicht man wie folgt

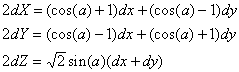
worin

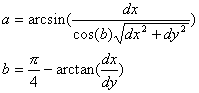
Dies ist aequivalent zu

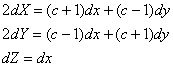
worin

Dann gilt

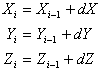
Für die Zipfel wird das i-te Volumenelement diesmal wie folgt berechnet:

worin

a die Distanz zwischen P_i-1 und P_i-1'

b die Distanz zwischen P_i und H

c der Höhenunteschied Z_i - Z_i-1

d die Distanz zwischen P_i' und P_i-1'

und H der Hilfspunkt

H = P_i'+(P_i-1 - P_i-1')

ist.

P' ist jeweils der Fusspunkt des Polygonpunktes P auf der Winkelhalbierenden in der Projektion (Z=0), dessen Koordinaten (m,m) man einfach durch Mittelwertbildung der beiden Koordinaten (r,s) von P gewinnt.

Die Berechnung des Quaders in der Mitte ist gleich wie bei Typ Ib.

Kissen vom Typ Ic

In der Abwicklung gelten folgende Beziehungen:

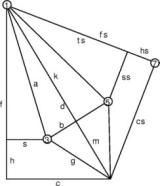
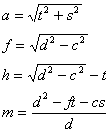
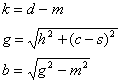
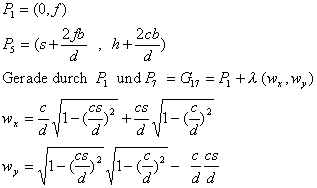
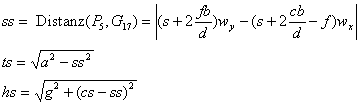
In einem senkrechten Schnitt durch die Pyramide parallel zur breiteren Pyramidenseite sollen folgende Bezeichnungen gelten.

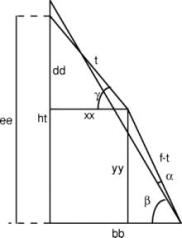
Bei gegebenem Abweichwinkel a des unteren Teils der schmalen Zipfelseite von der Pyramide ist

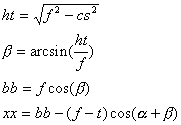
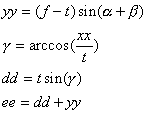
Gleiche Gleichungen gelten für die breite Zipfelseite: a' ... ee'.

Die Raumkoordinaten für P3 werden (xx,s,yy) und diejenigen für P5 (xx',ss,yy').

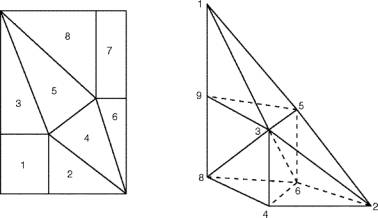
Die auf der linken Seite differenzierten Teilvolumina sind mit den Hilfspunkten von der rechten Seite wie folgt zu berechnen:

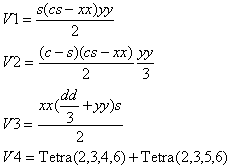
Tetra(1,2,3,4)=Determinante(P2-P1,P3-P1,P4-P1)/6

Bei vorgegebenen c=0.1985, cs=0.2193 und d=0.5460 aus dem Kissen Ib, wählte ich s und t und liess den Excel-Solver mit a und a' spielen bis die Zipfelhöhen ee und ee' in den beiden Seiten gleich gross ausfielen und gleichzeitig der Abstand zwischen Punkt 3 und 5 genau 2b betrug.

Ich änderte dann s und t so ab, dass der Volumengewinn am Zipfel durch Eindrücken der Kanten mit ca. 12% maximal ausfiel. Dies war für s=0.0836, t=0.413, a=0.2641 rad und a'=0.2749 rad der Fall und bringt für das gesamte Kissen mit 4 Zipfeln und einem unveränderten Quadermittelstück die schon erwähnten 7.6%.

Ein gleichzeitiges Neuoptimieren des Parameters cs, der dem t im Kissen Ib entspricht, bringt nichts, wie ich mit eine Sondierung mit +0.01 und -0.01 nachprüfte.