Ici 19 cylindres s'entrecoupent dont les axes passent par les coins opposés du polyèdre suivant

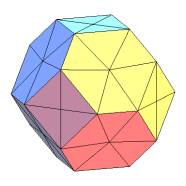
C'est un octaèdre tronqué et sont inclus les centres des faces. Le degré du tronquage est tel que l'isotropie des axes soit maximale. Ceci est atteint en choisissant des semidiagonales de 1/raçine(3) dans des carrés placés à distance 1 du centre du polyèdre.

Avec un rayon 1 pour les cylindres la surface de l'intersection vaut

12.61582235

et son volume un tiers de cela.

L'intersection a 504 faces.