Ici nous montrons une intersection de 17 cylindres dont les axes
traversent de coins opposés du polyèdre suivant
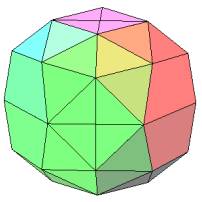
Il n'est pas simple de trouver un polyèdre
avec 17 paires de coins opposés et avec une régularité maximale. Celui-ci
est déduit du dodecaèdre en lui ajoutant 6 coins d'un octaèdre et 8 coins d'un cube.
Ceci était suivit d'un ajustage. Voir esquisse en bas.

Les cylindres ayant un rayon de un, la surface de l'intersection vaut
12.6115
et son volume un tiers de cela.
Il y a 388 facettes.
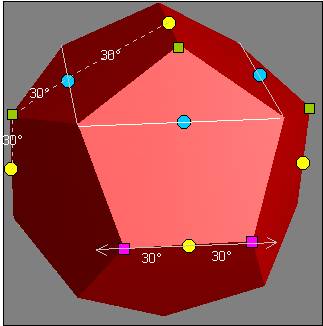
La construction du polyèdre à 34 coins: