Here 17 cylinders intersect with axes going
through opposite corners of the following polyhedra
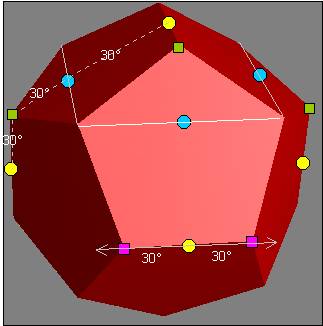
It is not easy to find polyhedra with 17 pairs
of opposing corners distributed regularily. This one is derived from the
dodecahedra (20 corners) where 6 octohedra- and 8 cube-corners were added and
relaxed. See scetch at the bottom.

With radius 1 the surface of the intersection
is
12.6115
and its volume is a third of the surface.
The intersection has 388 facets.
The construction of the 34 corner polyhedra: