Here 14 cylinders intersect with axes going through opposite corners of the following polyhedra

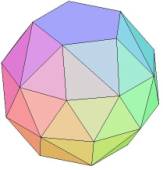
To get most isotropic oriented cylinder axes two pentagons and two nonagons are placed horizontally at optimal heigths, +b2 and –b2 for the pentagons and +b1 and –b1 for the nonagons. KD is the smallest distance between any corner.

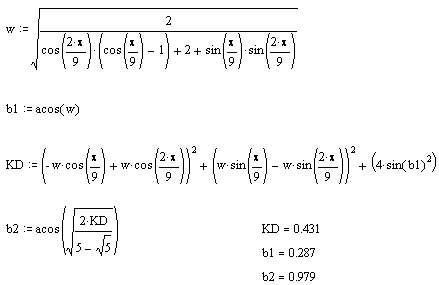
With radius 1 the surface of the intersection is

12.66527178

and its volume is a third of the surface.

Here follows a zoom of the encircled part

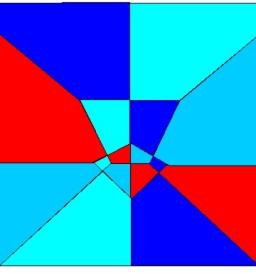
These very small facets complet the count of the facets generated by 14 cylinders which is exactly 14*(14-1)*2 = 364.

In this intersection of 14 cylinders we have 72 different facets which is far more than the usual about 20 facets for comparable intersections.