Fribourg, 6.1.2010 (updated 2.6.2010)

Counting colored polyhedra with the aid of the Polya-Burnside Lemma is well known. This time I had the idea to count face pairings of the platonic polyhedra. These face pairings are tilings with pairs of adjacent faces.

The tetrahedron has only one pairing.

The cube has 2 pairings:

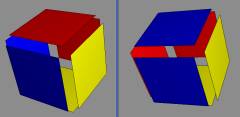
In reality this is only one pairing because one is the mirror of the other.

The octahedron too has 2 pairings:

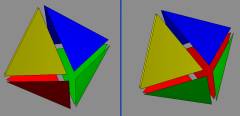
The icosahedron too has only 2 pairings!

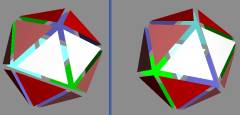
Doing the face pairing you cannot avoid the formation of two separated "hemispheres", the only tiling of such a hemisphere is evidently directed. So the two hemispheres can be turned only in two ways respective to each other (parallel or not). Put attention to the light colors white and cyan.

The dodecahedron is the most interesting case. This time we have 5 different pairings. I show them in the planar description. The outside of the scetch corresponds to the backside of the polyhedron.

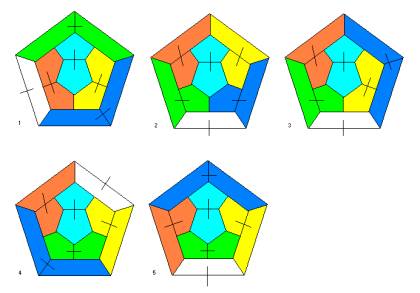
I found this counting by a brute force program constructing all tilings and eliminating doubles by applying the 60 possible rotations and 60 possible mirrorings.

Nick Baxter, California, did a Burnside analysis for me.

To do this, you have to look at each of the 60 permutations of the dodecahedron DDH. Then for each of these, how many ways to pair the faces appear the same after that permutation is applied.

There are five "families" of permutations, where each member of the family permutes the faces in the same way. These are:
Identity (1) - this is the permutation that does not change the shape
72 degree face rotation (12) - rotate to DDH with an axis through the center of a face and turn 72 degrees.
144 degree face rotation (12) - same but with 144 degree rotation.
180 degree edge rotation (15) - rotate around axis through center of opposite edges
120 degree vertex rotation (20) - rotate around axis through opposite vertices

By hand, I counted 125 ways to pair faces on a fixed DDH.
By hand, I counted 17 ways to pair faces so that they appear the same after an edge rotation.
By hand, I counted 5 ways to pair faces so that they appear the same after a vertex rotation.
There are no ways to pairs the faces so that they appear the same after either type of face rotation.

So N = (125 + 15*17 + 20*5)/60 = 8

Here 8 instead of 5 are found because the following 3 tilings which are mirrors of some of the 5 mentioned above are included (6 is mirror of 1, 7 of 3 and 8 of 4).

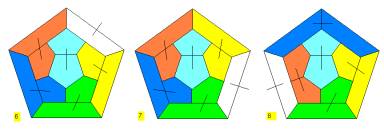
I show as an example the 5 face pairings which appear the same after a vertex rotation.

Non platonic polyhedra

Contribution of Enrico Bernal (Stuttgart, Germany, 2.6.2010)

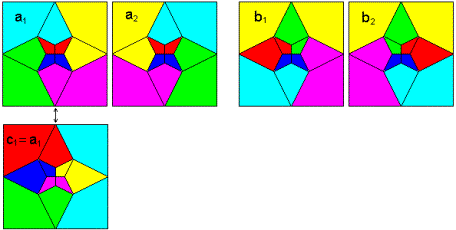
The Rhombododecahedron has 2 pairings (a and b):

Rhombotriacontahedron: work in progress.