6.1.1993
Folding stamps
I found the idea in
Michael
Holt, "Neue mathematische Aufgaben für Denker und Tüftler", Studio
Dumont 1988, Seite 27.
In how many ways n connected stamps (in a line) can be
folded?
The answer for 2, 3 and 4 is 1, 2 and 5 resp. See the
illustration.

5 stamps
can be folded in 14 ways:

6 stamps can be folded in 38 ways:

Finding the number of foldings for bigger n’s must be
done by a programm which can have the following steps
1) Scan
the list of all n! permutations of 1 2
3 .. n
2)
For each horizontally written permutation link 1 with
2 on top. This
separates de figures in different groups.
3)
Then
link 2 with 3 on bottom
4)
Now check if 3 and 4 are in the same group (above). If
not the permutation has failed and we try the next permutation. Otherwise link
3 with 4 and update the grouping.
5) Continue
beneath with figures 4 and 5.
6) and so
on
7) until
n is linked to n-1. If yout get here
you have a solution.
Let’s name the number of collected solutions in this
way 'brutto'.
Now we have to eliminate multiple solutions. We
consider that solution B which you get from solution A by flipping top/down is
not different.
We also consider that solution C which you get from
solution A by turning the strip of stamps by 180° first and applying the same
folding sa for solution A afterward is not different.
Also a combination of B and C is not different.
Let’s name this reduced folding number 'netto'.
Here is
a table with the numbers for one to 10 stamps
|
n |
n! |
brutto |
netto |
|
2 |
2 |
2 |
1 |
|
3 |
6 |
6 |
2 |
|
4 |
24 |
16 |
5 |
|
5 |
120 |
50 |
14 |
|
6 |
720 |
144 |
38 |
|
7 |
5040 |
462 |
120 |
|
8 |
40320 |
1392 |
353 |
|
9 |
362880 |
4536 |
1149 |
|
10 |
3628800 |
14060 |
3527 |
The ratio brutto/netto which measures the multiplicity
of solutions approaches 4 for big n’s.
Brutto
andd netto are growing by a factor of three for big n’s.
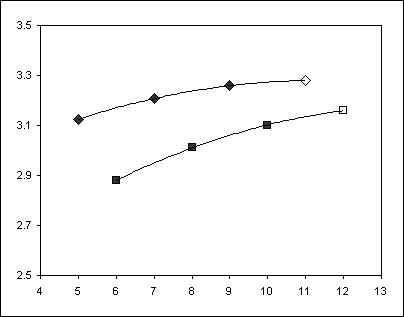
The function brutto(n)/brutto(n-1) shows an
alternating pattern. It is clear that the possible symmetries are different if
n is even or odd. If we separate the even and odd points to form two different
curves, we can nicely extrapolate for the 11 and 12 stamps and get approxiamtly
11’500 and 36’400 netto foldings resp.
![]()