6.1.1993
Marken falten
Die
Anregung stammt aus
Michael
Holt, "Neue mathematische Aufgaben für Denker und Tüftler", Studio
Dumont 1988, Seite 27.
Es geht
darum herauszufinden, auf wieviel Arten ein Streifen von n Marken zu einem
Stapel zusammengefaltet werden kann.
Hier
zunächst die Bilder für 2, 3 und 4 Marken mit b.z.w. 1, 2 und 5 Faltungen

5 Marken
können auf 14 Arten gefaltet werden

6 Marken
können auf 38 Arten gefaltet werden

Eine
Annäherung an die gesuchte Anzahl erhält man, wenn man folgenden Algorithmus
anwendet.
1)
Man
gehe die Liste aller n! Permutationen durch.
2)
Für
jede horizontal hingeschriebene Permutation verbinde man oben die 0 mit der 1,
wodurch die restlichen Zahlen in Gruppen zerfallen.
3)
Dann
verbinde man unten die 1 mit der 2.
4)
Anschliessend
prüfe man oben, ob 2 und 3 in der gleichen Gruppe sind. Wenn nicht kann man
bereits zur nächsten Permutation übergehen. Wenn ja, verbinde man 2 und 3 und
bringe die Gruppierungen oben auf den neuen Stand. Dies geht mit Inkrementieren
der Gruppennummer für alle Zahlen zwischen der 2 und der 3. Dabei ist das
Inkrement nach jeder Gruppenbildung zu
verdoppeln, wenn verhindert werden soll, dass getrennte Gruppen entstehen, die
die gleiche Nummer tragen.
5)
Jetzt
unten gleich verfahren für die Zahlen 3 und 4.
6) u.s.w.
7)
Bis
n mit n-1 verbunden werden kann. Dann liegt eine Lösung vor.
Wir
nennen die so gefundene Anzahl Lösungen 'brutto'.
Die
Lösungen sind nämlich jetzt noch zu reduzieren. Wir wollen Lösung B, die aus
Lösung A dadurch hervorgeht, dass der ganze Stapel um 180° gedreht wird, nicht
mitzählen.
Auch die
Lösung C nicht, die man gewinnt, wenn man zuerst den ganzen Streifen um 180°
dreht und dann die gleiche Faltung wie in A vornimmt.
Auch die
Kombination von B und C soll nicht gezählt werden.
Die
solchermassen bereinigte Anzahl wollen wir 'netto' nennen.
Hier
folgt die berechnete Anzahl Faltungen für alle Fälle bis zu zehn Marken.
|
n |
n! |
brutto |
netto |
|
2 |
2 |
2 |
1 |
|
3 |
6 |
6 |
2 |
|
4 |
24 |
16 |
5 |
|
5 |
120 |
50 |
14 |
|
6 |
720 |
144 |
38 |
|
7 |
5040 |
462 |
120 |
|
8 |
40320 |
1392 |
353 |
|
9 |
362880 |
4536 |
1149 |
|
10 |
3628800 |
14060 |
3527 |
Bei der
Bereinigung von brutto nach netto gehen
für grössere n drei Viertel der Lösungen weg.
Bei
steigendem n nehmen brutto und netto je um rund einen Faktor drei zu.
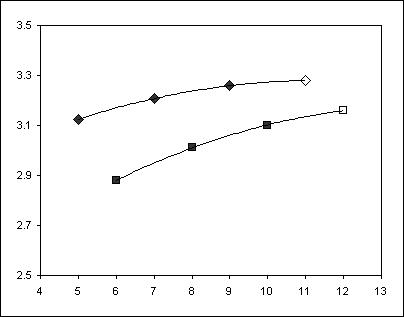
Bei der
Funktion brutto(n)/brutto(n-1) kann man einen Zickzackverlauf bemerken. Dies
hat damit zu tun, dass für eine gerade Anzahl Marken die Symmetrieverhältnisse
anders liegen als bei einer ungeraden Anzahl Marken. Wenn ich also die geraden
und ungeraden Fälle trenne, bekomme ich gutmütige Kurven, bei denen ich den
letzten Wert jeweils extrapoliert habe, was für die Fälle 11 und 12 Marken zu
ca 11’500 und 36’400 Faltungen führt.
![]()