Covering power
Introduction
In two places I have seen an interesting geometric problem. I try to generalize this problem here.
In the journal no 27 of the nederlandish puzzle club CFF the following problem is presented: how big can aquadratic table be and still be covered by three quadratic pieces of paper withside length one. The answer is given as the square root of the golden section.
In a book with the title “GoldenSection” (A.Beutelsbacher/B.Petri, Der goldene Schnitt, BI Wissenschaftsverlag) I have found a similar problem: how big can a circular table be and still be covered by five circular pieces of paper. The answer is that the ratio of the radius of the covered table to the radius of the covering sheets is the golden section.
Definition
The circle being a regular polygon with an infinity of sides one can include the two problems above in the following generalization.
covering power c(n,m) :=
ratio of the side of a maximal regular n-polygon Zahl, which can be covered by m regular n-polygons, to the side of those polygons.
This is a homogeneous case of an even more general one.
covering power c(n,m,k) :=
ratio of the side of a maximal regular k-polygon Zahl, which can be covered by m regular n-polygons, to the side of those polygons.
General properties
Let Phi be the golden section
![]()
![]()
then the above mentioned problems have the solutions
![]()
![]()
Certainly it can be proven that
There are ideal cases where we have no intersections
![]()
We have also
We find that for n<9 and m<8 (inf means infinity)
The problems don’t have only one global optimum but also local optima. In some cases I show the hopefully global optimum and some previous solutions.
If my solution is constructable with rule and compasses then I give a closed formula calculated by MathCad. For the othercases figures are calculated with iterative methodes.
Probabely there exists no pure algorithme to calculatethe covering power which can be programmed. You have to try very different ways to get good solutions but you can be helped by programs as the Solver in Excel. It is pleasant that the result of these problems can always be presented in easily readable geometric form.
Principles for the construction of solutions
Principle P1:
Principle P2:
Principle P3:
Here are my solutions sofar
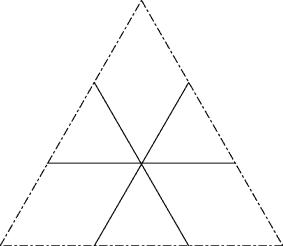
c33
Solution A:
Put together two triangles and align the common side vertically. Now push a triangle with horizontal base upwards without leaving the two first triangles.
![]()
Solution B:
This solution is more symmetric and more efficient
![]()
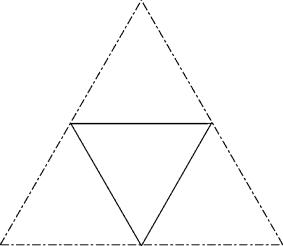
c34
Trivial.
c35, c36
c35 and c36 certainly are not bigger than c34.
c36 has a better solution. See Link to Friedman beneath.
c37
Add a row of 3 aequidistant and aligned triangles to the solution c34.
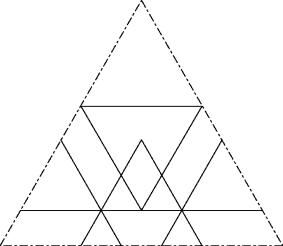
c37 has a better solution. See Link to Friedman beneath.
c38
Add a row of 4 aequidistant and aligned triangles tothe solution c34.
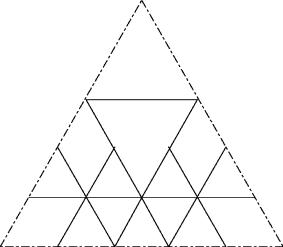
c38 has a better solution. See Link to Friedman beneath.
c39
Trivial.
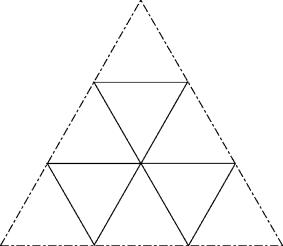
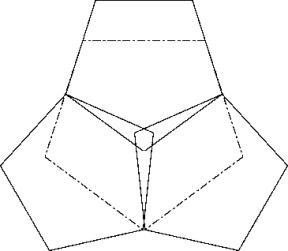
c43
The solution of the journal CFF.
![]()
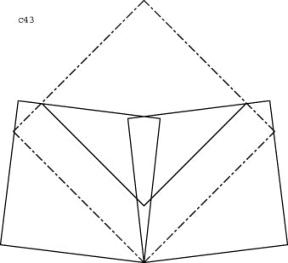
c44
Trivial.

c45, c46
c45 and c46 certainly are not bigger than c44.
c47
Solution A:
Add three non intersecting squares rotated by 45° totwo neigbouring sides of solution c44.
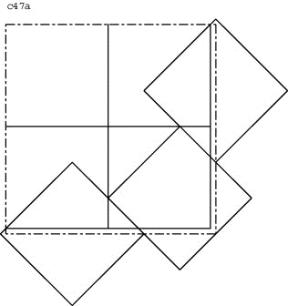
![]()
Solution B:
There is a much better solution. Do not turn the middle square of the added ones. If you optimize the turning angle of the two other added squares you find 45°.
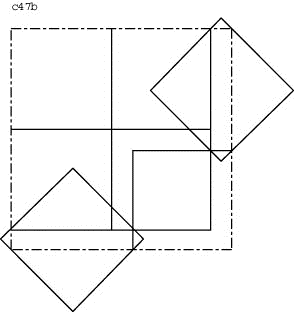
![]()
c48
Solution A:
Add four non intersecting squares rotated by 45° to two neigbouring sides of solution c44.
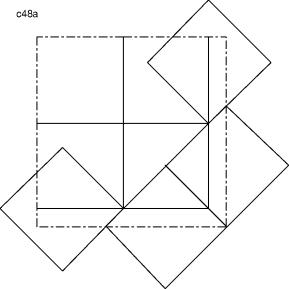
![]()
Solution B:
Push a pair of squares turned by 45° from a corner of the c44 solution outward in direction 45° as far as possible. Follow with the two remaining squares and turn them a litte bit.
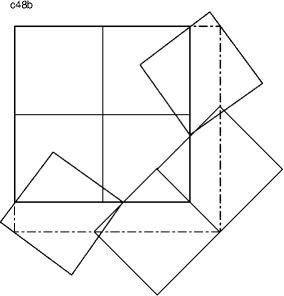
c49
Trivial.

c53
Solution A:
Put together two pentagons and align the common side vertically. Now push a pentagon with horizontal diagonal upwards without leaving the two first pentagons.
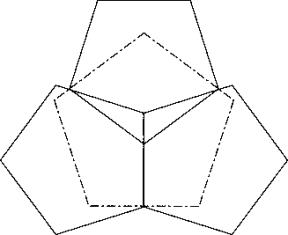
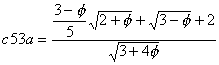
Solution B:
Principle P2.
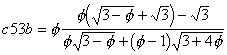
c54
I show three solutions with almost identical performance.
Apply the method of solution c53a not only on the top but also on the bottom and extend the covered pentagon to get solution A.
If you turn the covered pentagon in solution A by 90°you get solution B.
In the third solution (C) you start with three pentagons sharing two sides. Then you fill the remaining hole by a fourth pentagon.
Solution A:
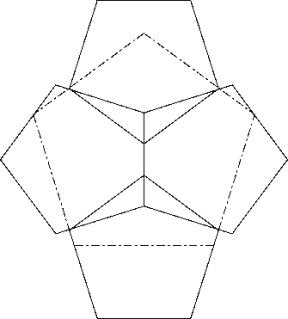
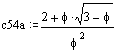
Solution B:
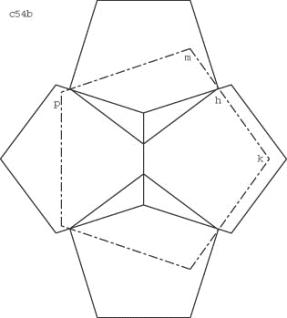
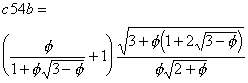
Solution C:
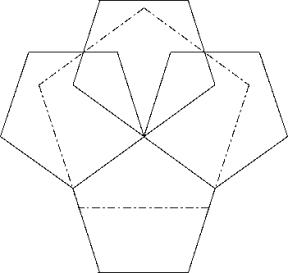
![]()
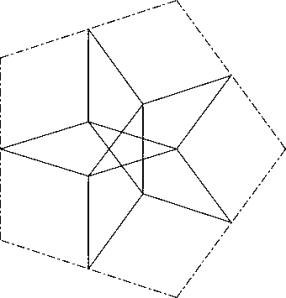
c55
This is the central symmetric solution without a hole in the middle.
![]()
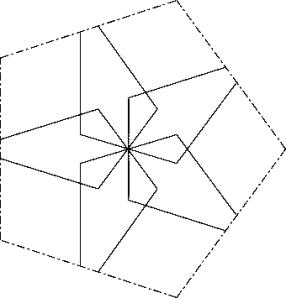
c56
This is the central symmetric solution where the outer sides of the pentagons don’t intersect.
c57
Following principle P1 form a star with 6 pentagons. Fill the hole in the middle with the seventh pentagon. Laying down the big pentagon you have two possibilities. a) put a corner of the big pentagon in the corner of a small pentagon or b) put a corner of the big pentagon in the throat of the star.
The two solutions are very close. a) ist only inferior to b) by 0.2 %. Solution a) has a covering power of 2.0982.
We show here only solution b) with a covering power of2.1029.
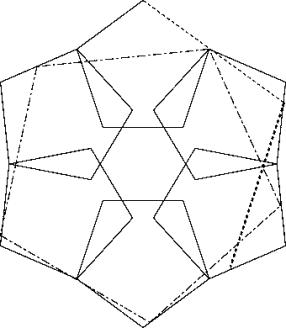
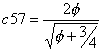
c63
Solution B where the diagonals of three hexagons form a triangle has a lot of overlapings but is superior to solution A where three hexagons are put together without any overlaping.
![]()
Solution B:
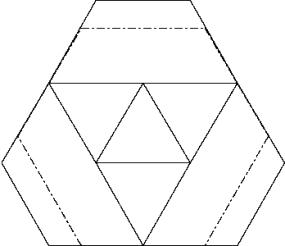
![]()
c64
Put together two hexagons with a common horizontal side. This defines the placement of a bigger hexagon whose wings can be covered by two more hexagons. Pushing the last two hexagons more outside doesn’t bring any benefit.
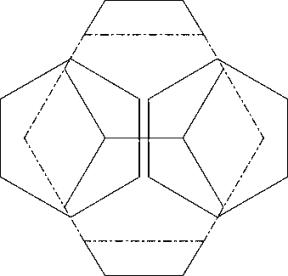
c65
Applying principle P1 and P2 gives a symmetricsolution A.
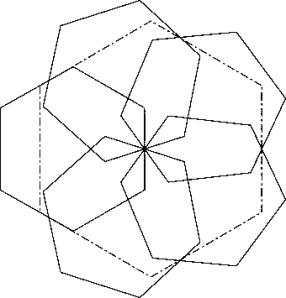
![]()
We have doubled overlappings in the middle in this solution. So we can push the top hexagon upward and the bottom one downward toget a better solution B.
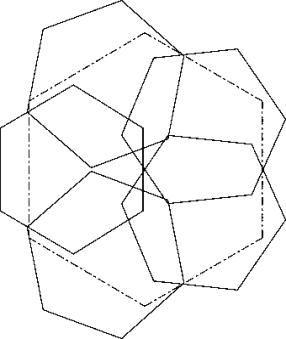
An other local optimum can be found when starting with solution A. Shift the left hexagon outward then rearrange the two hexagons at right. This gives solution C which is superior to A but not to B.
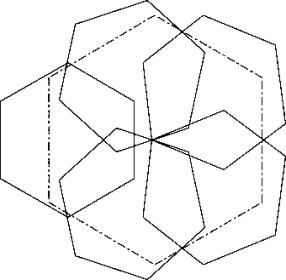
Enrico Bernal from Stuttgart has sent me the following solution which is clearly better (29.5.2008):
c66
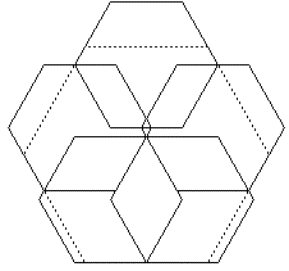
Take the constellation of the solution of c67 in the next chapter and push the 6 outer hexagons together until the middle hexagon can be taken appart.
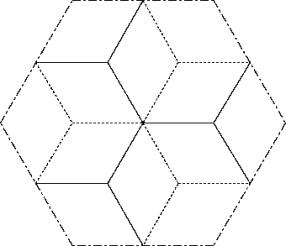
c67
It’s simply a part of the regular hexagonal grid without any overlaping.
![]()
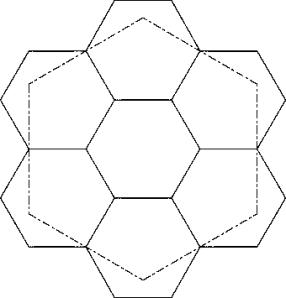
c73
This solution comes straightforward with principle P1 and P2.
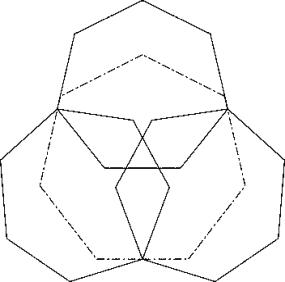
c74
Arrange the big diagonals of the heptagons in a square. Put only in the top pentagon the bigger part of the heptagon outward. Apply principle P2 and you get solution A.
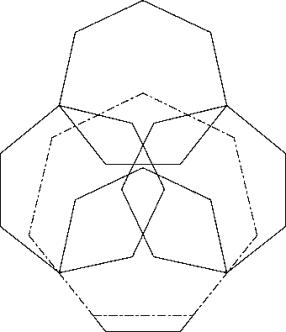
In this solution there is room on the top. Shifting the big heptagon upward gives a better solution B.
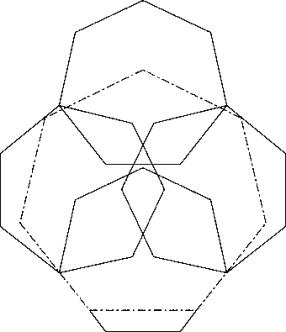
Turning the left and right heptagon around the two bottom cornes of the square brings a further augmentation of the covering power and solution C.
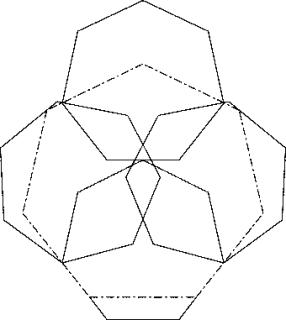
Enrico Bernal from Stuttgart has sent me the following solution which is better (29.5.2008):
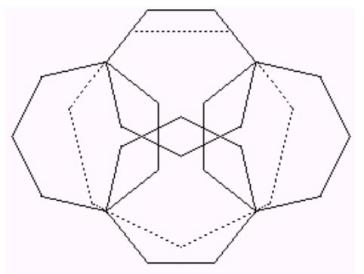
c75
Apply principle P1 and form a pentagon with the big diagonal of 5 heptagons. The bigger part of the heptagons must be turned inward. We are left with a hole. Push all heptagons together to fill this hole.Then applying principle P2 we solution A
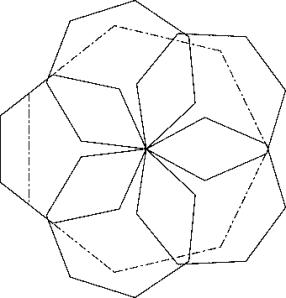
Now push the top heptagon downward and the bottom one upward to create an overlaping which allows to push to the right the two right heptagons. This is solution B.
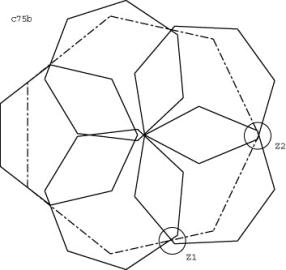
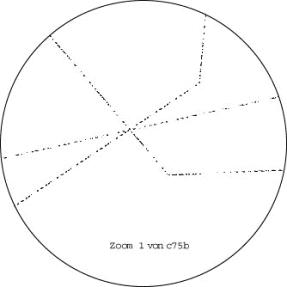
Here we exceptionnaly show two zooms
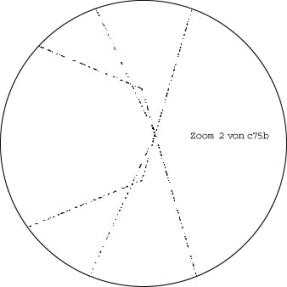
If you shift alternatively a corner of the big heptagon in the outer half of an small heptagon, you get solution c75c
which is better than c75a.I think you can't exploit the the gained space on the other side.
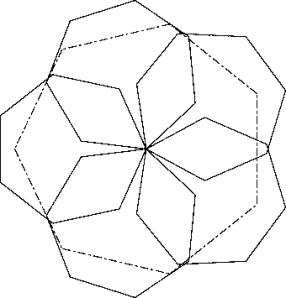
c76
Apply principle P1 and form a pentagon with the big diagonal of 5 heptagons. The bigger part of the heptagons must be
turned inward. We are left with a hole. Fill this hole with the sixth heptagon. Now you can put a big heptagon in two
different ways.
Solution A: Put a corner of the big heptagone as far as possible towards the left in the left heptagon. Then this corner is almost exactly 4 units away from the opposite throat (3.9987902) when the side of the small heptgons is scaled to 1.
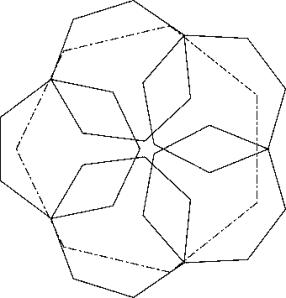
Solution B: If instead of this we apply principle P2 (here in the bottom right small heptagon) then the opposite corner of the big heptagon lays exactly in the throat. This solution is only slightly worse than c76a.
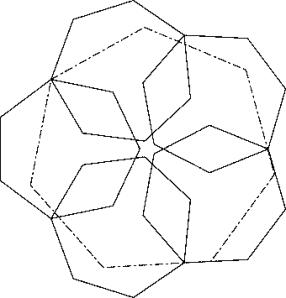
In solution A it can be observed that the big heptagon doesn’t go through the throat. Compressing the solution horizontally and extending a little bit vertically gives solution C.
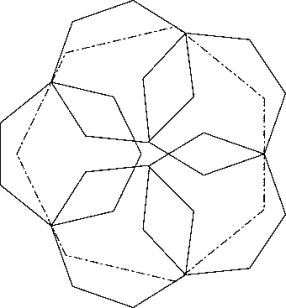
If now in the bottom and top heptagon the bigger partist turn outward and we optimize again by compressing horizontally and extending verticaly then we get solution D
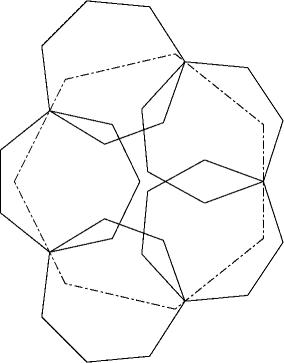
But not using the last heptagon to fill the centralhole gives a better solution. Form a hexagon with the diagonals of the six heptagons and push them together until the central hole diapears. Since you have doubled overlapings in the middel you can push aoutward everey second heptagon. A final optimization of two heptagons gives solution D where all six throats are touched by the big heptagon.
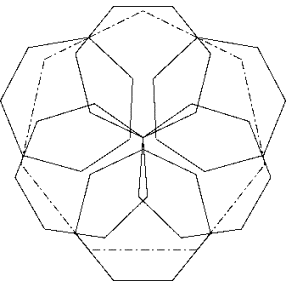
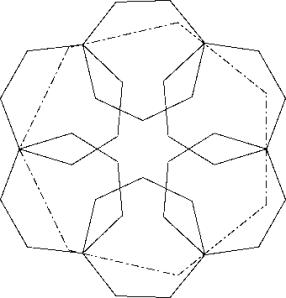
c77
Form a hexagon with the diagonals of the six heptagons with bigger parts inside. Cover the hole in the middle with the seventh heptagon. Lay the middle of a side of the big heptagon against a throat. This gives solution A.
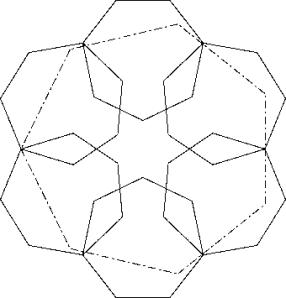
Not all throats are touched so a further optimization gives solution c77a1.
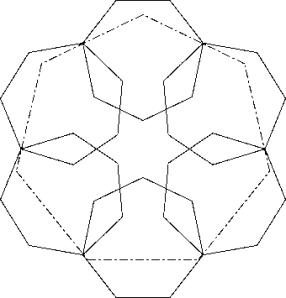
It is better to apply principle P2. This gives solution c77b.
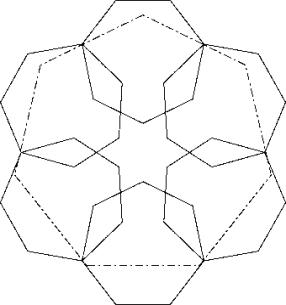
The throat again are not perfectly touched so the solution can be enhanced to give c77b1.
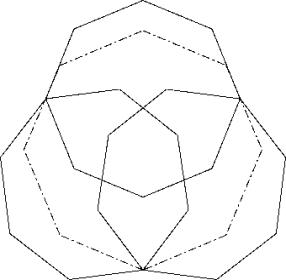
c83
Applying principle P1 and P2 gives.
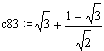
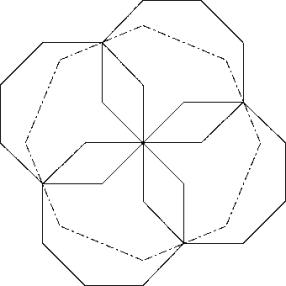
c84
For this case principle P1 gives
![]()
c85
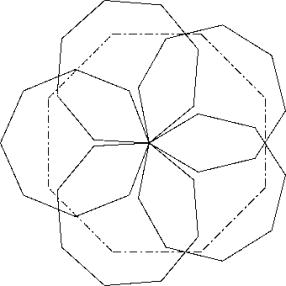
Draw a regular pentagon with sides as long as the diagonal of the octogon. Lay down the octogons with their diagonal on this pentagon. You are left with a hole in the middle. Push the octogons together to fill this hole. Now you have three possibilities:
A) Follow principle P2
B) Put the middle of side of the big octogon on a throat.
C) Push a corner of the big octogone in a small octogon.
Case B ist the best
Becouse two throats are not touched some optimization is possible.
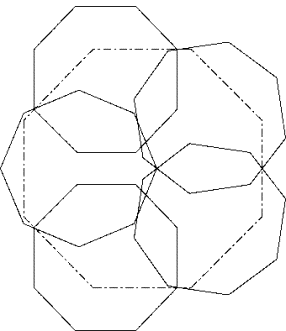
Details of this optimization:
Push the left octogon slightly to the right. Now the two octogons to the right can be turned outward around the throatpoint at right. Finally positions of the octogons on top and bottom are optimized.
Some figures for the constellation:
Let the origin of a system of coordinates be in the center of the left octogone and let the octogons have sidelength 1, then the center of the octogon at top right has the coordinates (2.18587702, 0.85020782) and his diagonal forms an angle of -14.182403° with the x-axis and the center of the octogon at top has the coordinates (0.44639586, 1.49191151) and his diagonal forms an angle of -22.481958° with the x-axis. Hence two sides of this octogon are almost perfectly parallel to the x-axis.
c86
Draw a regular pentagon with sides as long as thediagonal of the octogon. Lay down the octogons with their diagonal on this pentagon. You are left with a hole in the middle which can easily be covered bythe sixth octogon. Now you have two possibilities:
Solution A: Push a corner of the big octogone in asmall octogon.
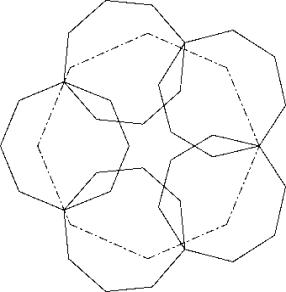
Solution B: Put the middle of side of the big octogon on a throat.
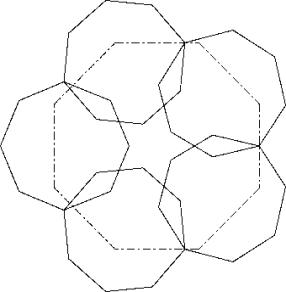
Hence solution Bis slightly better than solution A.
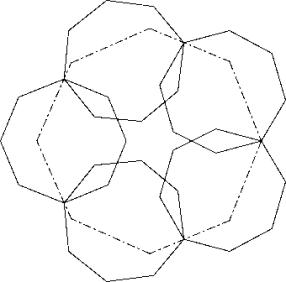
In solution A not all throats are touched so anoptimization is possible
In solution B too not all throats are touched so an optimization is possible
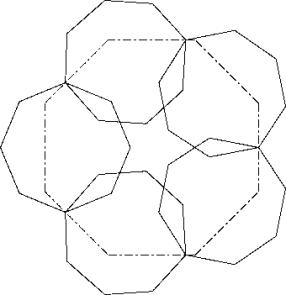
It is better to not keep one octogone to fill a hole in the middle. Forming a crown of 6 octogons and squeezing it to avoid a hole in the middle (principle P1 and P3) gives a better solution. For the optimization every second octogon can be pushed outward. Finally two the position of two octogons must be adapted. In the solution alle throats are touched.
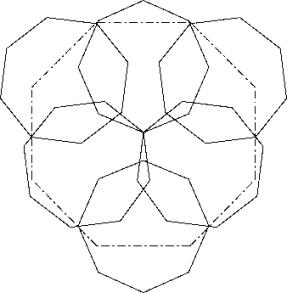
c87
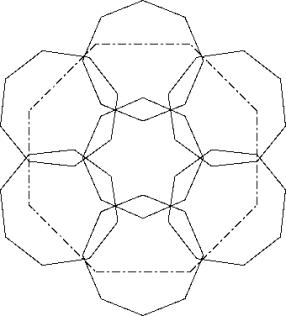
Draw a regular hexagon with sides as long as the diagonal of the octogon. Lay down the octogons with their diagonal on this pentagon. You are left with a hole in the middle. Push the octogons a little together (P3) so that the hole can be covered by the seventh octogon. Now we apply principle P2 and get the solution A.
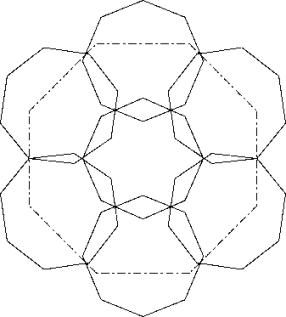
The two throats at left and right are not touched. Hence an optimization is possible and gives solution B.
cCircle3
In the following
cCircleX =cKreisX = c(inf,X)
A crown of three circles must be squeezed until the circle centers lie on the border of the two other circles.
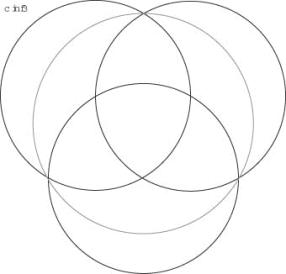
![]()
this is different from
![]()
cCircle4
Principle P1 and P3 gives immediatly the solution
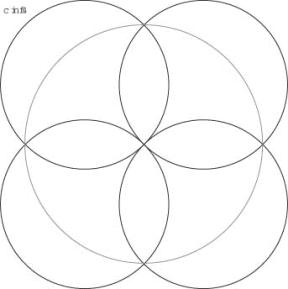
![]()
cCircle5
Principle P1 and P3 gives immediatly the solution
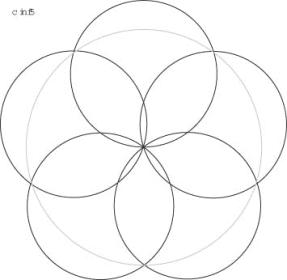
![]()
The general formula 2 cos (Pi/n) gives the golden section for n=5.
cCircle5 has abetter solution! See Link to Friedman beneath.
cCircle6
Put the centers of 5 circles on a pentagon of side 1and fill the central hole with a sixth circle. Let vary the radius of the circles between 0.5 and 1 and you will observe that the corresponding coveringpower has a maximum at radius = ![]() . The maximum value is
. The maximum value is
for solution A.
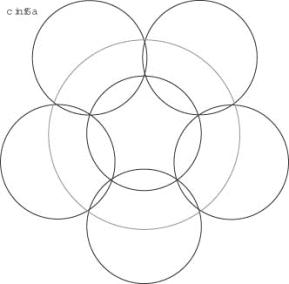
There exists an other special radius where the middle circle is just big enough to cover the hole. With this radius the coveringpower is exactly phi=1.6180.. hence smaller than in solution A.
But finaly a solution without a hole in the middle is superior. Solution B.
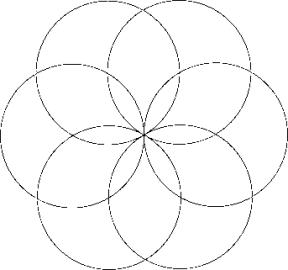
![]()
cCircle6 has a better solution! See Link to Friedman beneath.
cCircle7
This time the solution with a hole in the middle covered by the seventh circle is best. Here again varing the radius of the circles (and having the side of the hexagon fixed at 1) gives a maximumcovering power at a special radius.
Solution A
cCircle7a=2 (best)
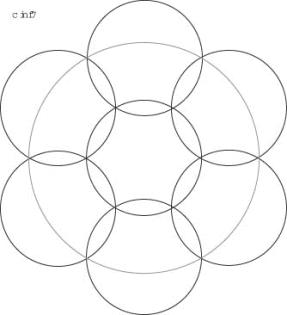
The special radius where we have the optimum is ![]() .
.
The solution B without a covered hole in the middle is inferior
![]()
Further investigation
Enrico Bernal from Stuttgart in Germany has sent the following superior solutions.
Better solution for c(4,8)
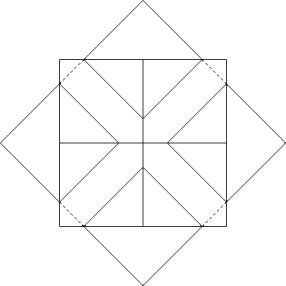
This very symetric solution has a covering power of
![]()
this equals 2.414.. and is bigger than the 2.327.. ofthe best solution so far.
Better solution for c(5,4)
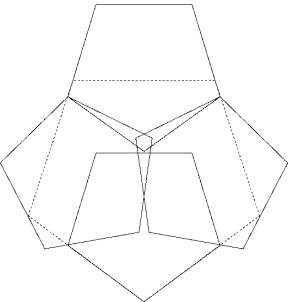
This solution has a covering power of
![]()
this equals 1.5073.. and is bigger than the 1.409.. of the best solution so far.
The pentagons on both sides are turned by
Better solution for c(5,7)
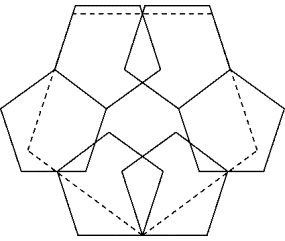
This solution has a covering power of
![]()
this equals 2.157.. and is bigger than the 2.1029.. of the best solution so far.
Bernal mentioned that the solution can be optimized. I did it and got the following solution
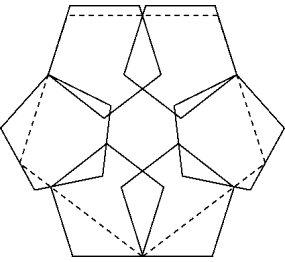
This solution has a covering power of
![]()
The pentagons on both sides are turned by
10.9784421..°
Better solution for c(6,4)
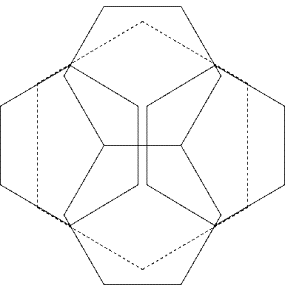
This solution has a covering power of
![]()
this equals 1.53.. and is bigger than the 1.5 of the best solution so far.
Here is a table of the best covering powers so far
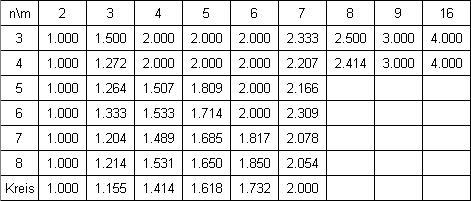
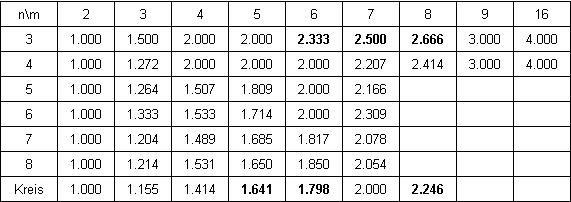
The following table shows 6 cases in bold where better solutions are presented in Erich Friedman’s Packing Center.
https://erich-friedman.github.io/packing/squcosqu/
https://erich-friedman.github.io/packing/tricovtri/
Please let me know if you find better solutions.