Covering power
Einleitung
An zwei verschiedenen Stellen bin ich einem interessanten Geometrieproblem begegnet, das ich hier verallgemeinern möchte.
In der Zeitschrift des holländischen Puzzle-Klubs CFF No 27 (Ladder competition No4) wird das Problem mit den drei quadratischen Tischtüchern präsentiert. Mit ihnen kann man bestenfalls einen Wurzel(goldener Schnitt) grösseren quadratischen Tisch zudecken.
Aus einem Buch über den Goldenen Schnitt (A.Beutelsbacher/B.Petri, Der goldeneSchnitt, BI Wissenschaftsverlag) kenne ich ein analoges Problem mit 5 kreisrunden Tischtüchern, die bestensfalls einen kreisrunden Tisch bedecken können, der im Verhältnis des goldenen Schnittes grösser ist als die Tücher(diesmal ohne Wurzel).
Definition
Weil der Kreis weitgehend einem regelmässigen Polygon mit unendlich viel Seiten entspricht, möchte ich folgende Funktion definieren.
covering power c(n,m) :=
Zahl, die bemisst, um wieviel ein n-gonaler Tisch grösser sein darf, wenn er durch m n-gonale Tücher bedeckt werden soll.
Es ist ein homogener Fall, weil man noch folgenden heterogenenFall in Betracht ziehen könnte
covering power c(n,m,k) :=
Zahl, die bemisst, um wieviel ein k-gonaler Tisch grösser sein darf, wenn er durch m n-gonale Tücher bedeckt werden soll.
Allgemeine Eigenschaften
![]()
![]()
dann gilt für die eingangs erwähnten zwei Probleme
![]()
![]()
Ich glaube, dass man beweisen kann, dass
Dann gibt es diverse Fälle mit überlappungsfreien Lösungen wie
![]()
Es gilt sicher auch
Es stellt sich heraus, dass für alle n<9 und m<8 gilt
Neben dem globalen Optimum hat es oft fast gleichwertige lokale Optima. In gewissen Fällen zeige ich neben dem (hoffentlich) globalen Optimum auch Vorstufen oder Nachbaroptima.
Wo die Lösung mit Zirkel und Lineal kontruierbar ist, habe ich für das Bedeckungsvermögen eine Formel hergeleitet (unter Zuhilfenahme von MathCad). Für die andern Fälle habe ich relativ genaue Werte mit der analytischen Geometrie und iterativen Verfahren ermittelt.
DieBeschäftigung mit dieser Aufgabenstellung illustriert gut, wie der menschliche Geist auf interessante Weise mit der dienstbaren künstlichen Intelligenz zusammenwirken kann. Die Aufgabenstellung ist sehr konkret und kann einfach formuliert werden. Das Resultat ist auch wieder sehr anschaulich. Dazwischen muss viel mühselig erarbeitet werden. Hier kann der PC sehr stark mithelfen und zwar nicht nur bei einfachen arithmetischen Berechnungen sondern auch in den algebraischen Herleitungen von Formeln, sowie bei der Durchführung iterativer Vorschriften der analytischen Geometrie zum Auffinden von optimalen Konstellationen.
Die hier behandelte Aufgabenstellung verlangt die Erfindung vieler qualitativ verschiedener Lösungsansätze, die nicht notwendig auseinander hervorgehen,und die ohne tatkräftige Mithilfe eines Computers schwerlich gegeneinander ausgespielt werden könnten.
Konstruktionsideen
Für die Konstruktion von Lösungen sind folgende Mittel (Leitideen) nützlich
Leitidee L1:
Leitidee L2:
Leitidee L3:
Die einzelnen Fälle
c33
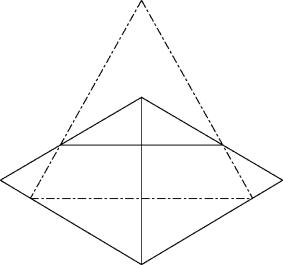
Lösung A:
Zwei Dreiecken mit gemeinsamer senkrechter Seite (also ohne Ueberlappung) ein Dreieck mit waagrechter Basis so aufsetzen, dass die Basis in den beiden ersten Dreiecken bleibt.
![]()
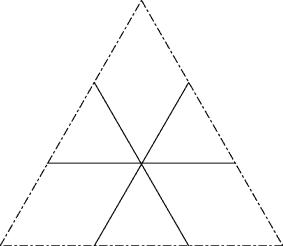
Lösung B:
Zentralsymetrische Anordnung (L1)
![]()
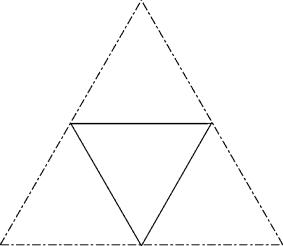
c34
Trivial.
c35, c36
c35 und c36 sind sicher nicht grösser als c34.
c36 hat eine bessere Lösung. Siehe Link zu Friedman am Schluss.
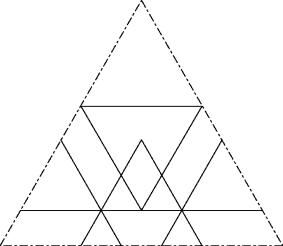
c37
Dem c34 eine Reihe von 3 aequidistanten und gleich ausgerichteten Dreiecken anfügen
c37 hat eine bessere Lösung. Siehe Link zu Friedman am Schluss.
c38
Dem c34 eine Reihe von 4 aequidistanten und gleich ausgerichteten Dreiecken anfügen
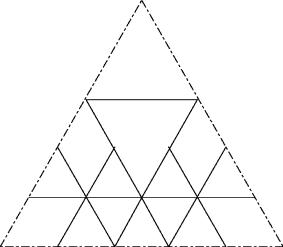
c38 hat eine bessere Lösung. Siehe Link zu Friedman am Schluss.
c39
Trivial.
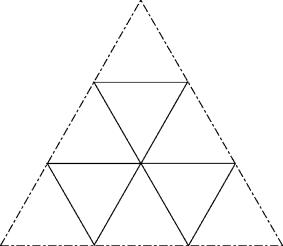
c43
Lösung aus CFF.
![]()
c44
Trivial.

c45, c46
c45 und c46 sind sicher nicht grösser als c44.
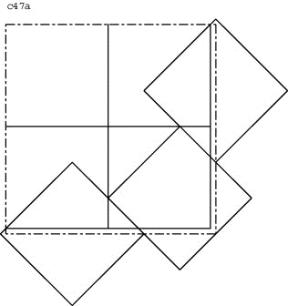
c47
Lösung A:
Drei um 45°gedrehte, nicht überlappende Quadrate an zwei anliegende Seiten von c44 anfügen.
![]()
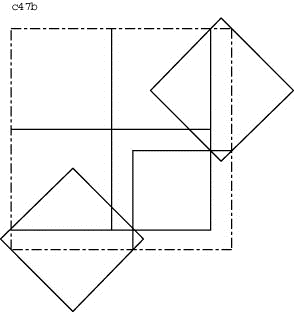
Lösung B:
Es gibt eine deutlich überlegenere Variante von c47a. Dazu wird das mittlere der hinzugefügten Quadrate nicht gedreht. Bei Freigabe des Winkels der zwei andern Quadrate erweist sich, dass 45° optimal sind.
![]()
c48
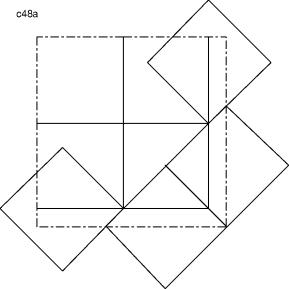
Lösung A:
Vier um 45°gedrehte, nicht überlappende Quadrate an zwei anliegende Seiten von c44 anfügen
![]()
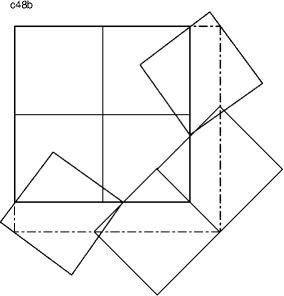
Lösung B:
Ein um 45°gedrehtes, nicht überlappendes Quadratpaar an einer c44-Ecke A soweit nachaussen schieben (in 45° Richtung) bis die Verlängerung der c44-Seiten, die nicht durch A gehen, durch die geeignet platzierten letzten zwei Quadrate gleich weit bedeckt bleiben wie die Seiten, die durch A gehen. Die dabei sich bildenden Kehlen sind noch nicht kritisch.
c49
Trivial.

c53
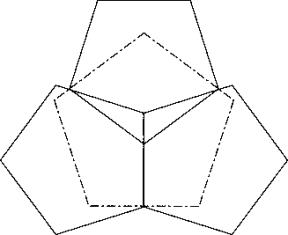
Lösung A:
Ausgehend von zwei Pentagonen mit gemeinsamer Seite (also ohne Ueberlappung), die horizontal angeordnet zu denken sind, oben die Diagonale des Pentagons horizontal heranführen, bis sie die beiden Pentagone berührt. Dann das dazugehörige Pentagon mit dem grösseren Teil nach aussen zeichnen.
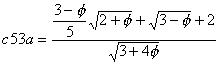
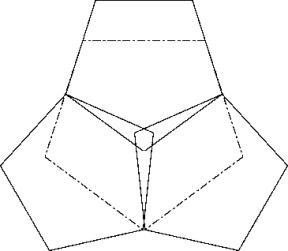
Lösung B:
Leitidee L2.
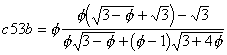
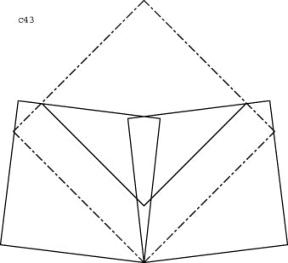
c54
Ich will drei Lösungsansätze präsentieren, von denen zwei nur leicht unterlegen sind.
Ausgehend von zwei Pentagonen mit gemeinsamer Seite (also ohne Ueberlappung), die horizontal angeordnet zu denken sind, oben und unten die Diagonale des Pentagons horizontal heranführen, bis sie die beiden Pentagone berührt. Dann das dazugehörige Pentagon mit dem grösseren Teil nach aussen zeichnen. Diesmal ergeben sich Ueberlappungen.
In dieses Gebilde aus 4 Pentagonen kann ein Pentagon aufrecht (d.h. mit horizontaler Basis, Lösung A) oder liegend (90° gedreht, Lösung B) eingeschrieben werden. Im ersten Fall haben wir eine typische Verkeilungdes grossen Pentagons in einem kleinen Pentagon.
Die dritte Lösung C geht von einem Pentagon aus, an das an zwei benachbarten Seiten je ein Petagon ohne Ueberlappung angefügt wird. Die übrigbleibende keilförmige Lücke wird durch ein viertes Pentagon abgedeckt.
Lösung A:
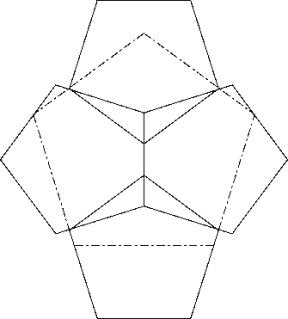
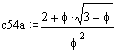
Lösung B:
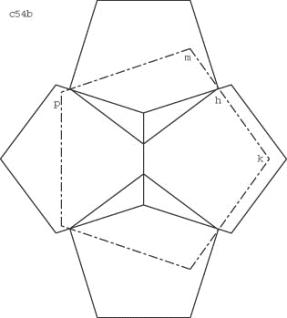
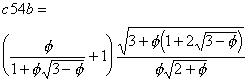
Lösung C:
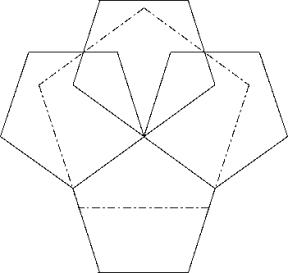
![]()
Die zentralsymetrische Anordnung, bei der in der Mitte keine Lücke bleibt.
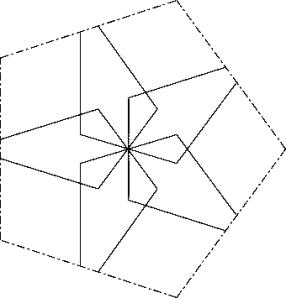
![]()
Die zentralsymetrische Anordnung, bei der die äusseren Seiten ohne Ueberlappung aneinanderstossen.
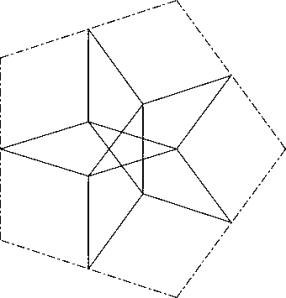
Gemäss L1 mit 6 der 7 Pentagone hexagonal anordnen. Die Lücke mit dem siebten Pentagon abdecken. Beim Hineinlegen des grossen Pentagons ergeben sich zwei Möglichkeiten. a) Die Ecke in eine Sternecke legen oder b) Die Ecke in eine Sternkehle legen.
a) ist b) nur ganz knapp unterlegen um ca. 0.2 %. Der Faktor beträgt im Falle a) 2.0982. Er ergibt sich, wenn die Seite der Sternecke mit einer Seite der konvexen Nachbarecke geschnitten wird. Wenn die Diagonale des Eckpentagons mit einer Seite des übernächsten Pentagons geschnitten wird, ergibt sich der Faktor 2.1292. Dieses Grosspentagon ragt aber knapp aus dem Stern heraus.
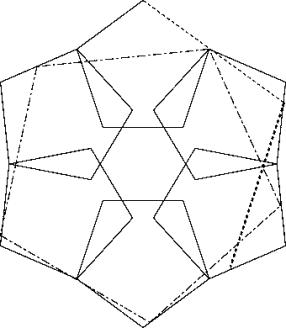
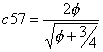
c63
Die Lösung B mit den zu einem Dreieck angeordneten Diagonalen hat sehr viel Ueberlappung ist aber der Lösung A mit drei an einer Ecke nahtlos aneinandergefügten Hexagonen überlegen.
![]()
Lösung B:
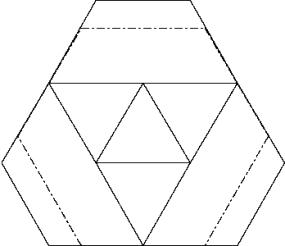
![]()
c64
Lösung durch Verkeilung (L2) in zwei benachbarten, nicht überlappenden Hexagonen. Die zwei andern Hexagone können etwas weiter aussen gelegt werden als in der Skizze. Dies bringt aber keinen zusätzlichen Gewinn für c64.
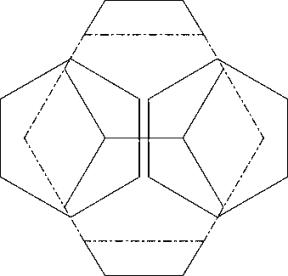
c65
Die mit (L1) und(L2) konstruierte Lösung ist symmetrisch und ergibt.
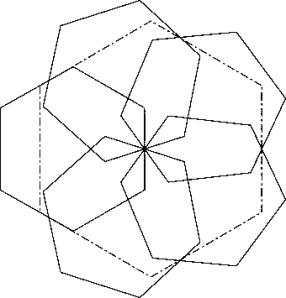
![]()
Man sieht bei dieser Lösung, dass wegen den z.T. doppelten Ueberlappungen in der Mitte zwei nicht benachbarte Kleinhexagone nach aussen versetzt werden dürfen. Damit habe ich folgende verbesserte Lösung erzielen können.
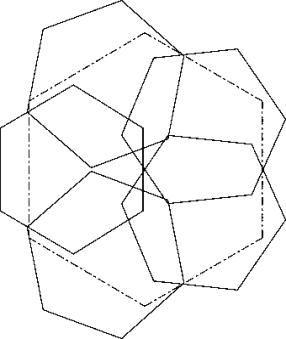
Eine andere Lösung, bei der das linke Hexagon nach aussen geschoben wird und die beiden rechten mit einer Ecke in die Mitte gelegt werden und dann derart nach aussengedreht werden, dass die Kehle rechts erhalten bleibt, ist der symmetrischen Lösung c65a ebenfalls überlegen.
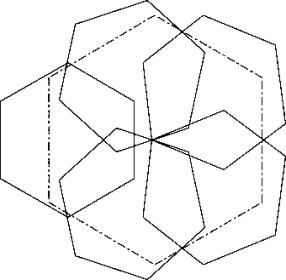
Enrico Bernalaus Stuttgart hat mir folgende deutlich verbesserte Lösung zukommen lassen(29.5.2008):
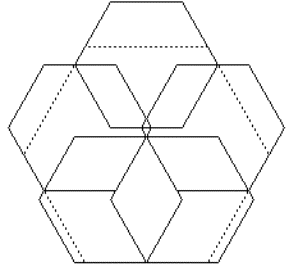
c66
Die Konstellation von c67 einfach zusammenschieben bis das mittlere siebte Hexagon überflüssig wird. In diesem Moment berühren sich die äusseren Seiten zweier benachbarter Hexagone gerade noch.
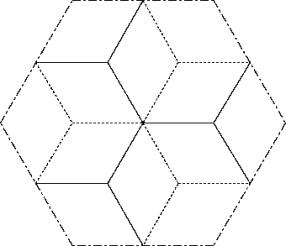
c67
Es ist ein Ausschnitt von sieben Hexagonen aus dem Bienenwabengitter ohne jegliche Ueberlappung zwischen den Hexagonen.
![]()
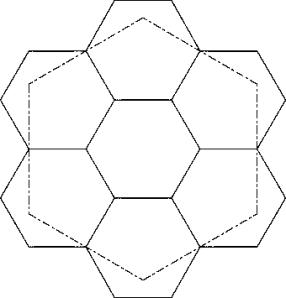
c73
Realisation mit Leitidee L1 und L2.
Wahrscheinlich kann kein Ausdruck ohne Winkelfunktionen für c73 berechnet werden.
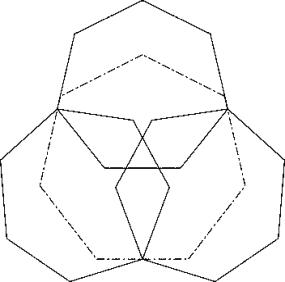
c74
Zuerst wurden die grössten Diagonalen in einem Viereck angeordnet. Dabei wurde nur beim oberen Heptagon die grössere Hälfte nach Aussen gelegt. Beim arbeiten mit dem Schnittpunkt der unteren und oberen Verkeilgeraden ergab sich eine erste Lösung
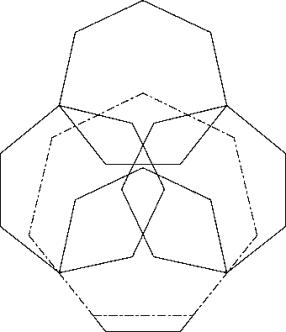
Weil es oben gar nicht zu einer Verkeilung kam, kann etwas gewonnen werden, wenn die Verkeilung unten weniger tief gestaltet wird.
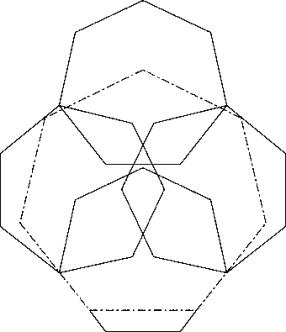
Eine weitere Verbesserung konnte erzielt werden, indem die beiden seitlichen Heptagone geeignet um die unteren Viereckpunkte nach aussen gedreht wurden. Dabei wurden die oberen Viereckpunkte etwas nach unten geholt.
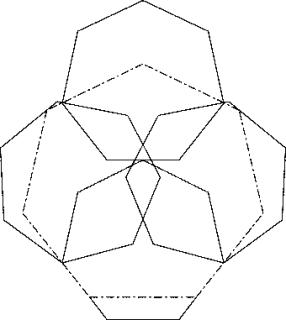
Enrico Bernalaus Stuttgart hat mir folgende verbesserte Lösung zukommen lassen (29.5.2008):
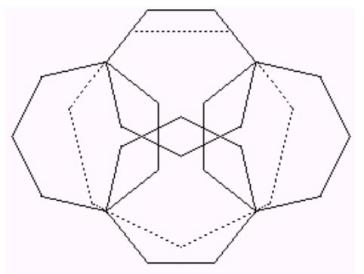
c75
Ein regelmässiges Pentagon erstellen, dessen Seiten gleich gross sind wie die Grossdiagonale des regelmässigen Heptagons mit Seite 1. Die fünf Heptagone mit ihren Grossdiagonalen auf dieses Pentagon legen mit der grösseren Hälften nach innen. Es bleibt eine Lücke, die man schliessen kann, indem die Heptagone zusammengeschoben werden. Wenn jetzt ein Grossheptagon verkeilt (L2) wird, erhält man Lösung A.
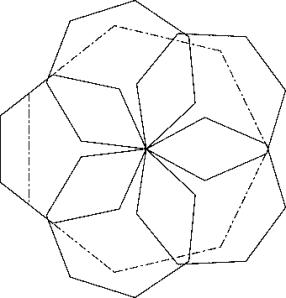
Man sieht, dass man die Nachbarheptagone des Verkeilheptagons wegschieben kann so, dass in der Mitte eine Ueberlappung entsteht, die durch Wegschieben der letzten beiden Heptagone wieder abgebaut werden kann. Man kann c75 dabei um etwa 0.04 vergrössern.
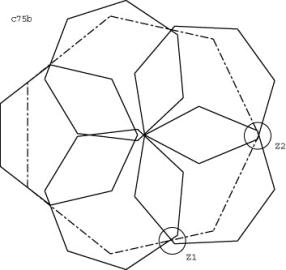
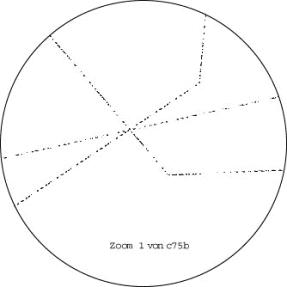
Hier zeigen wir ausnahmsweise 2 Zooms
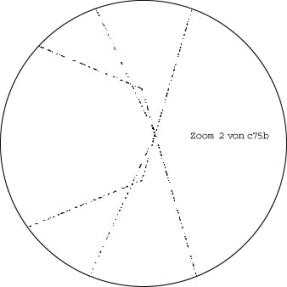
Wenn alternativ eine Ecke des Grossheptagons zentral und anschlagend in die äussere Hälfte eines Kleinheptagons gelegt wird, gewinnt man ein c75c, dass etwas grösser ist als c75a. Hier kann aber meines Erachtens die Reserve auf der gegenüberliegenden Seite nicht in eine Steigerung des c75c umgesetzt werden.
c76
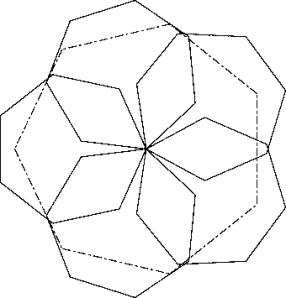
Ein regelmässiges Pentagon erstellen, dessen Seiten gleich gross sind wie die Grossdiagonale des regelmässigen Heptagons mit Seite 1. Fünf Heptagone mit ihren Grossdiagonalen auf dieses Pentagon legen mit der grösseren Hälften nach innen. Es bleibt eine Lücke, die durch das sechste Heptagon mühelos abgedeckt werden kann. In dieses Gebilde kann ein möglichst grosses Heptagon auf zwei Arten hineingelegt werden.
Lösung A: Eine Ecke des Grossheptagons zentral und anschlagend in die äussere Hälfte eines Kleinheptagons legen. Erstaunlicherweise ist dieser Eckpunkt dann fast genau 4 Einheiten vom gegenüberliegenden Kehlpunkt entfernt (nämlich 3.9987902 Einheiten). Grössenbestimmend ist in der Folge der Schnittpunkt einer Kleindiagonalen durch diesen Eckpunkt mit der äusseren Hülle der Kleinheptagone.
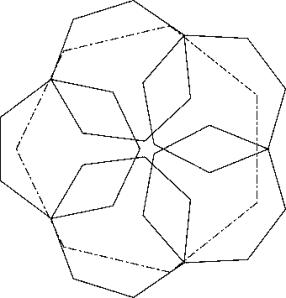
Lösung B: Alternativ kann das Grossheptagon in einem Kleinheptagon verkeilt werden (L2). Die gegenüberliegende Ecke des Grossheptagons geht dann genau durch einen Kehlpunkt der äusseren Hülle der Kleinheptagone, was grössenbestimmend ist. Diese Lösung ist nur wenig schlechter als c76a.
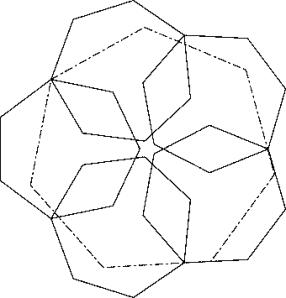
In der Lösung A kann man beobachten, dass die der zuerst gewählten Ecke des Grossheptagons gegenüberliegende Seite nicht durch eine Kehle geht. Man kann also noch etwas erreichen, indem das Pentagon in dieser Richtung zusammengedrückt und senkrecht dazu ausgebaucht wird. Dies führt zur Lösung C
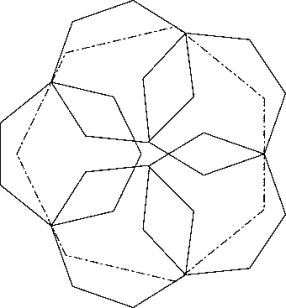
Wenn zwei der Kleinheptagone mit der grösseren Hälfte nach aussen gelegt werden, wird neu der Schnittpunkt einer Kleindiagonale durch den ersten Eckpunkt mit einer Geradendurch die übernächste Kehle, die die Richtung der übernächsten Seite hat, grössenbestimmend. Das Zusammendrücken und Ausbauchen des Pentagons muss neubestimmt werden. Wir erhalten die Lösung D
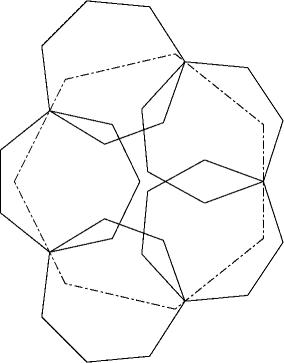
Es erweist sich, dass der zentralsymetrische Ansatz(L1), bei dem in der Mitte keine Lücke gelassen wird (L3), nach Optimierung eine bessere Lösung ergibt. Die Optimierung besteht darin, dass jedes zweite Siebeneck nach aussen geschoben werden darf wegen der doppelten Ueberlappungen in der Mitte. Dies geschieht so weit, bis die Diagonale des Siebenecks auf der Hülle der nicht bewegten drei Siebenecke liegt. Zwei der Siebenecke werden dann auf der Hülle noch zurecht geschoben. In der Lösung berührt das zugedeckte Grosssiebeneck alle sechs Kehlen.
c77
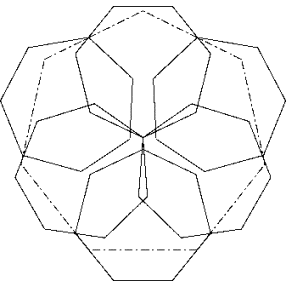
Ein regelmässiges Hexagon erstellen, dessen Seiten gleich gross sind wie die Grossdiagonale des regelmässigen Heptagons mit Seite 1. Die sechs Heptagone mit ihren Grossdiagonalen auf dieses Pentagon legen mit der grösseren Hälften nach innen. Es bleibt eine Lücke, die durch das siebte Heptagon mühelos abgedeckt werden kann. Wenn jetzt ein Grossheptagon mit einer Seitenmitte an eine Kehle gelegt wird, erhält man Lösung A.
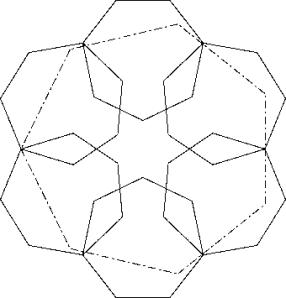
Diverse Kehlen werden nicht berührt, sodass mit einer Deformierung des Hexagons noch etwas gewonnen werden kann.
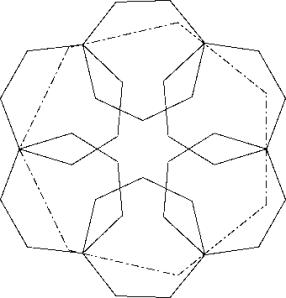
Wenn alternativ eine Ecke des Grossheptagons verkeilt wird (L2), gewinnt man ein c75b, dass etwas grösser ist als c75a.
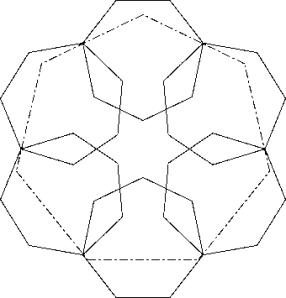
Zwei Kehlen werden nicht berührt, sodass mit einer Deformierung des Hexagons noch etwas gewonnen werden kann.
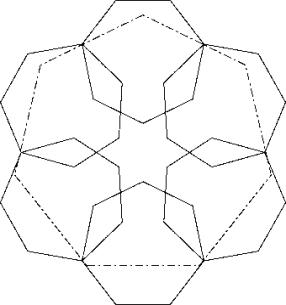
c83
Realisation mit Leitidee L1 und L2.
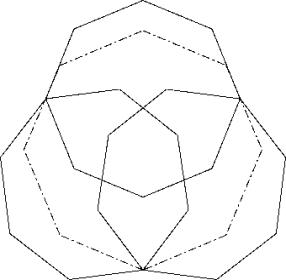
c84
Realisation mit Leitidee L1.
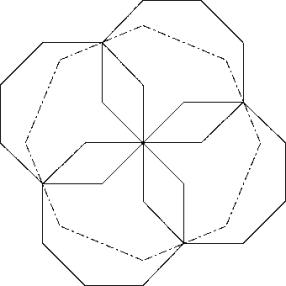
![]()
c85
Einregelmässiges Pentagon erstellen, dessen Seiten gleich gross sind wie die Diagonale des regelmässigen Achtecks mit Seite 1. Die fünf Achtecke mit ihren Diagonalenauf dieses Pentagon legen. Es bleibt eine Lücke, die man schliessen kann, indem die Achtecke zusammengeschoben werden. Von den drei Lösungsversuchen
A) Ein grosses Achteck verkeilen (L2)
B) Die Seitenmitte des grossen Achtecks in eine Kehle legen
C) Eine Ecke des grossen Achtecks zentral und mit den Armen anschlagend in die äussere Hälfte eines Kleinachtecks legen
ergab B) das grösste Bedeckungsvermögen
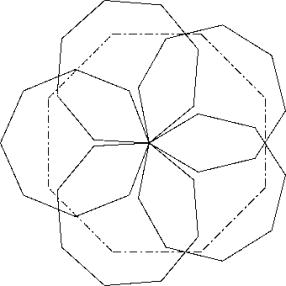
Weil zwei Kehlennicht berührt werden, kann durch eine Feinoptimierung noch etwas gewonnen werden.
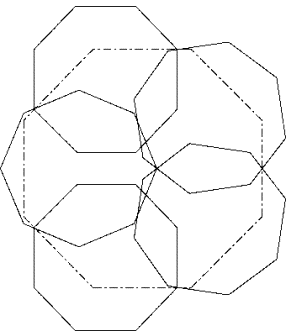
Die Optimierung erfolgte wie folgt. Das linke Achteck wurde optimal in die Konstellation hinein (nach rechts) geschoben. Damit konnten die beiden rechten Achtecke um die rechte Kehle nach aussen gedreht werden. Anschliessend wurden die verbleibenden zwei Achtecke mit zwei opponierenden Punken passend auf die äussere Hülle der bisherigen Achtecke gelegt.
Bezogen auf das Zentrum des linken Achtecks und bei Seitenlänge gleich eins, hat das Zentrum des Achtecks oben rechts die Koordinaten (2.18587702, 0.85020782) und seine Diagonale ist um -14.182403 Grad gegen die x-Achse geneigt und das Zentrum des Achteckes oben mitte hat die Koordinaten (0.44639586, 1.49191151) und seine Diagonale ist um -22.481958 Grad gegen die x-Achse geneigt. Es ist also fast genau achsenparallel (dazu wären -22.5 Grad nötig). Die unteren Achtecke sind Spiegelbilder der oberen.
c86
Ein regelmässiges Pentagon erstellen, dessen Seiten gleich gross sind wie die Diagonale des regelmässigen Achtecks mit Seite 1. Fünf Achtecke mit ihren Diagonalen auf dieses Pentagon legen Es bleibt eine Lücke, die durch das sechste Achteck mühelos abgedeckt werden kann. In dieses Gebilde kann ein möglichst grosses Achteck auf zwei Arten hineingelegt werden.
Lösung A: Eine Ecke des grossen Achtecks zentral und mit den Armen anschlagend in die äussere Hälfte eines Kleinachtecks legen. Grössenbestimmend ist in der Folge die gegeüberliegende Kehle.
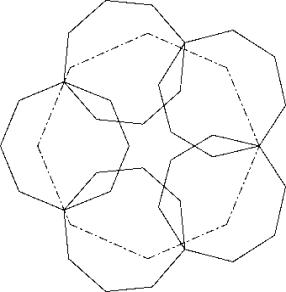
Lösung B: Alternativ kann die Mitte einer Seite des grossen Achtecks in eine Kehle der kleinen Achtecke gelegt werden. Grössenbestimmend ist dann eine Nachbarkehle, bei der die Hälfte einer Kleindiagonalen des grossen Achtecks herausgelesen werden kann.
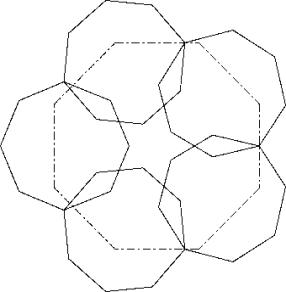
In der Lösung A kann man beobachten, dass zwei der Kehlen das grosse Achteck nicht berühren. Wieder kann durch ein Verändern der Winkel im Pentagon das Bedeckungsvermögen gesteigert werden. Dies führt zur Lösung A1
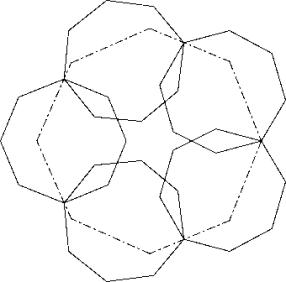
Auch in der Lösung B kann man beobachten, dass zwei der Kehlen das grosse Achteck nichtberühren. Wieder kann durch ein Verändern der Winkel im Pentagon das Bedeckungsvermögen gesteigert werden. Dies führt zur Lösung B1.
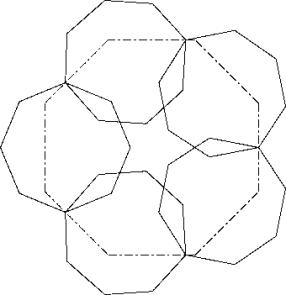
Es erweist sich, dass der zentralsymetrische Ansatz(L1), bei dem in der Mitte keine Lücke gelassen wird (L3), nach Optimierung eine bessere Lösung ergibt. Die Optimierung besteht darin, dass jedes zweite Achteck nach aussen geschoben werden darf wegen der doppelten Ueberlappungen in der Mitte. Dies geschieht so weit, bis die Diagonale des Achtecks auf der Hülle der nicht bewegten drei Achtecke liegt. Zwei der Achtecke werden dann auf der Hülle noch zurecht geschoben. In der Lösung berührt das zugedeckte Grossachteck alle sechs Kehlen.
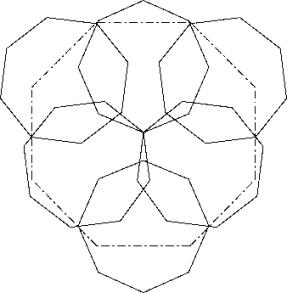
c87
Ein regelmässiges Hexagon erstellen, dessen Seiten gleich gross sind wie die Diagonale des regelmässigen Achtecks mit Seite 1 (L1). Sechs Achtecke mit ihren Diagonalen auf dieses Hexagon legen. Es bleibt eine Lücke, die durch das siebte Achteck nicht ganz abgedeckt werden kann. Wir schieben die sechs Achtecke genausoviel zusammen (L3), dass die Lücke abgedeckt werden kann. Wenn jetzt (L2) angewandt wird erhält man die Lösung A.
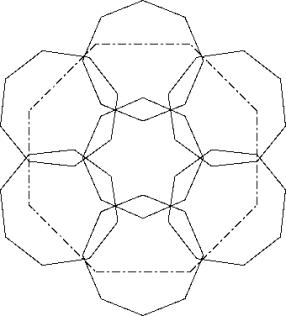
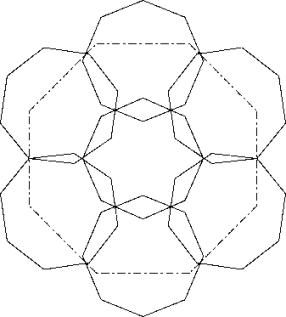
Man kann in dieser Lösung beobachten, dass das grosse Achteck die Kehle rechts nicht berührt. Wenn das Achteck rechts oben so nach oben verschoben wird, dass die obere Spitze des Sechsersterns in der Mitte sich nicht verändert, kann das einschreibbare Achteck vergrössert werden. Die Achtecke oben links, unten rechts und unten links müssen gleichzeitig entsprechend geschoben werden. Dies führt zur Lösung B.
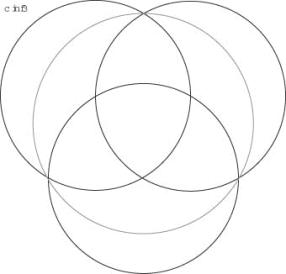
cKreis3
Bei der zentralsymetrischen Anordnung gibt es einen für das Bedeckungsvermögen optimalen Ueberlappungsgrad. Dies ist dann der Fall, wenn jeder Kreismittelpunkt auf den beiden andern Kreisen liegt.
![]()
dies ist verschieden von
![]()
cKreis4
Die Lösung ist die zentralsymetrische Anordnung, die gerade keine Lücke mehr offen lässt in der Mitte.
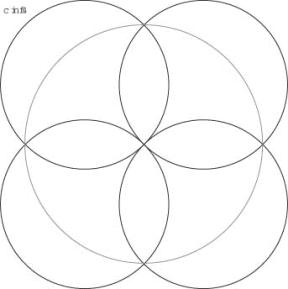
![]()
cKreis5
Die Lösung ist die zentralsymetrische Anordnung, die gerade keine Lücke mehr offen lässt in der Mitte.
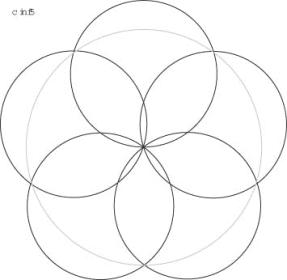
![]()
cKreis5 hat eine bessere Lösung! Siehe Link zu Friedman am Schluss.
cKreis6
Ich habe zunächst die Lösung verfolgt, bei der 5 Kreise auf die Eckpunkte eines Pentagons gesetzt werden und die Lücke in der Mitte mit einem weiteren Kreisbedeckt wird. Das Bedeckungsvermögen hängt dabei vom Kreisradius ab, der bei einer Pentagonseite von 1 zwischen 0.5 und 1 varieren darf. Die Funktion durchläuft ein Maximum. Es tritt beim Radius ![]()
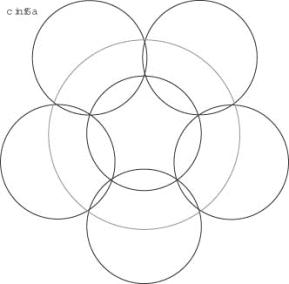
Natürlich gibt es einen Kreisradius, bei dem die Lücke in der Mitte gerade noch abgedecktwerden kann. Für diesen Kreisradius wird das Bedeckungsvermögen genau Phi (wiecKreis5)!
Dann hat sich herausgestellt, dass die symmetrische Anordnung wie in cKreis5 überlegen ist.Die Verhältnisse sind da sehr einfach.
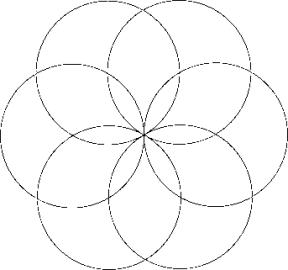
![]()
cKreis6 hat eine bessere Lösung. Siehe Link zu Friedman am Schluss.
cKreis7
Diesmal ist die Lösung, bei der 6 Kreise auf die Eckpunkte eines Hexagons gesetzt werden und die Lücke in der Mitte mit einem weiteren Kreis bedeckt wird, dem Lösungstyp von cKreis4,5,6 überlegen. Das Bedeckungsvermögen hängt dabei vom Kreisradiusab, der bei einer Pentagonseite von 1 zwischen 0.5 und 1 varieren darf. Die Funktion durchläuft ein Maximum. Es beträgt
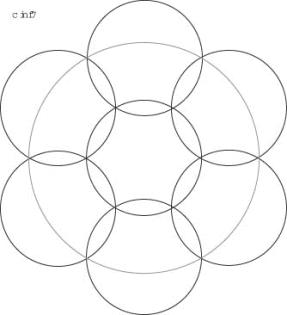
Dieses Optimum tritt beim Radius ![]()
Der Wert bei der symmetrischen Anordnung wie in cKreis5 beträgt
![]()
Nachtrag
Von EnricoBernal aus Stuttgart habe ich folgende interessanten Beiträge erhalten.
Eine neue bessere Lösung für c(4,8)
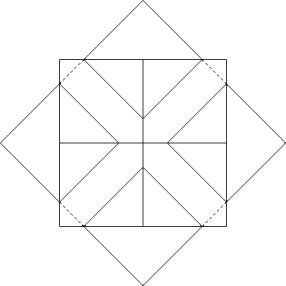
Diese sehr symmetrische Anordnung liefert einen Wert von
![]()
der mit 2.414..grösser ist als mein bisheriger bester Wert von 2.327..
Eine neue bessere Lösung für c(5,4)
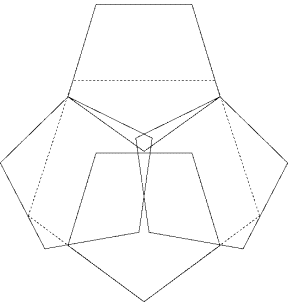
Diese
![]()
der mit 1.5073..grösser ist als mein bisheriger bester Wert von 1.409..
Die seitlichen Pentagone sind um
Eine neue bessere Lösung für c(5,7)
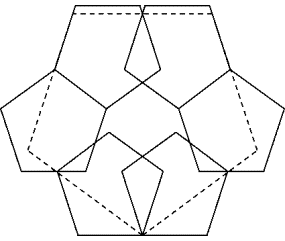
Diese
![]()
der mit 2.157.. grösser ist als mein bisheriger bester Wert von 2.1029..
Bernal hat angemerkt, dass man an dieser Anordnung noch etwas herumschrauben kann. Ich habe das getan und erhalte
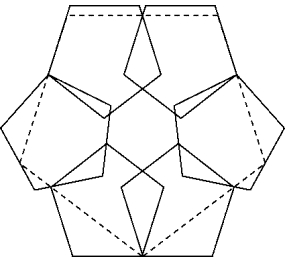
Diese
![]()
Die seitlichen Pentagone sind um 10.9784421..° verdreht. (Die obere Ecke des seitlichen Pentagons ist Drehpunkt und er liegt 1.30086221 von der darunter befindlichen Ecke des grossen Pentagons entfernt).
Eine neue bessere Lösung für c(6,4)
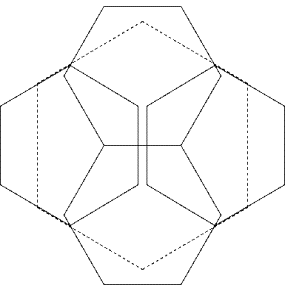
Diese
![]()
der mit 1.53..grösser ist als mein bisheriger bester Wert von 1.5.
Zusammenstellungder besten Lösungen bisher
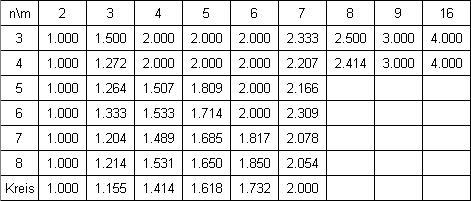
Es folgt eine Tabelle mit 6 verbesserten Werten (in Fettdruck), die ich Erich Friedman’sPacking Center entnehmen konnte
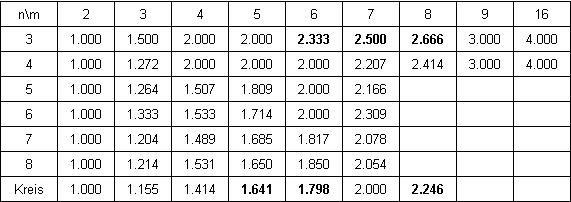
Wer kann das eine oder andere Problem besser lösen?